There are reactions in which the concentration of a reactant increases and decreases with time periodically. This type of behavior is associated with autocatalytic stages. In 1920 AJ Lotka proposed a simple mechanism in which the concentrations of components X and Y oscillate periodically. Lotka's mechanism is as follows:
\begin{equation} A+X\stackrel{k_1}{\rightarrow} 2X \end{equation} \begin{equation} X+Y\stackrel{k_2}{\rightarrow} 2Y \end{equation} \begin{equation} Y\stackrel{k_3}{\rightarrow} B \end{equation}
The oscillating behavior of this system is observed if the concentration of A is kept constant, therefore it is necessary to add A to the same rate that is spent.
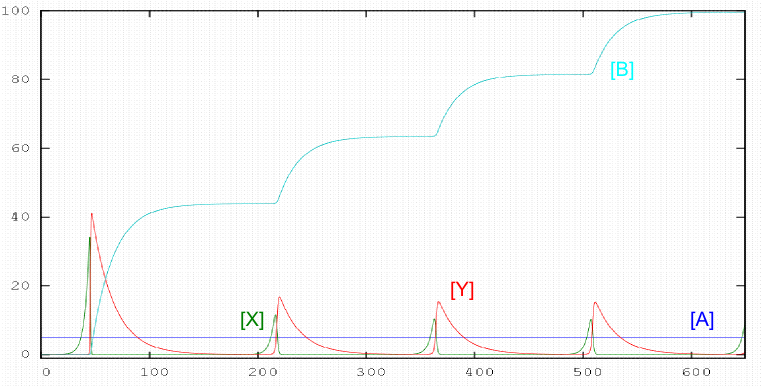
One of the most studied systems is the oregonator, proposed by Field and Noyes in 1974. The mechanism consists of 5 stages:
\begin{equation} A+Y\stackrel{k_1}{\rightarrow} X \end{equation}
\begin{equation} X+Y\stackrel{k_2}{\rightarrow} P \end{equation}
\begin{equation} B+X\stackrel{k_3}{\rightarrow}2X+Z \end{equation}
\begin{equation} 2X\stackrel{k_4}{\rightarrow}Q \end{equation} \begin{equation} Z\stackrel{k_5}{\rightarrow}Y \end{equation}
These 5 stages combine in proportion {1,1, 2,1,2} to give the overall reaction: $A+2B\rightarrow P+Q$ The plot was obtained for the following values of kinetic constants and initial concentrations: $k = \left(2.1, 2\times 10^9, 10^4, 4\times 10^7, 1\right)$ $\left([A], [B], [X], [Y], [Z], [P], [Q]\right) = \left(1, 1, 0, 0, 0.1, 0, 0 \right)$



