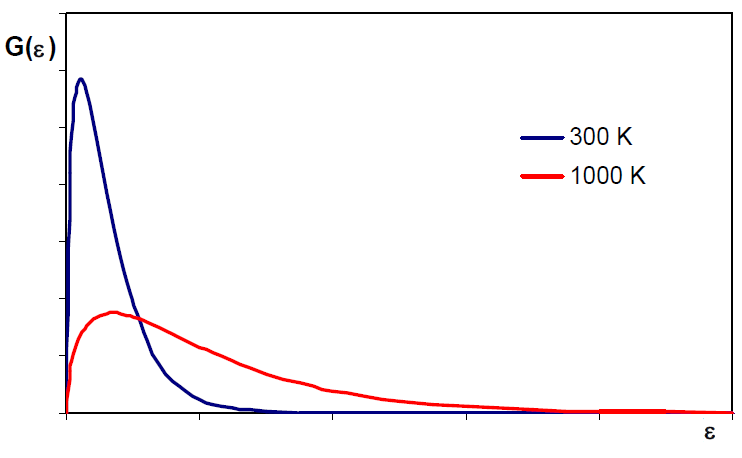
La distribución de Maxwell puede escribirse en función de energías traslacionales $\epsilon_{tr}=\frac{1}{2}mv^2$, despejando v, $v=\left(\frac{2\epsilon_{tr}}{m}\right)^{1/2}$, derivando: \begin{equation} dv=\left(\frac{2}{m}\right)^{1/2}\frac{1}{2}\epsilon_{tr}^{-1/2}d\epsilon_{tr}=\left(\frac{1}{2m}\right)^{1/2}\frac{d\epsilon_{tr}}{\epsilon_{tr}^{1/2}} \end{equation} Sustituyendo v y dv en $\frac{dN_v}{N}=\left(\frac{m}{2\pi mkT}\right)^{3/2}e{\frac{-mv^2}{2kT}}4\pi v^2dv$ \begin{equation} \frac{dN_{\epsilon_{tr}}}{N}=\left(\frac{m}{2\pi mkT}\right)^{3/2}e^{\frac{-m(2\epsilon_{tr}/m)}{2kT}}4\pi \left(\frac{2\epsilon_{tr}}{m}\right)\left(\frac{1}{2m}\right)^{1/2}\frac{d\epsilon_{tr}}{\epsilon_{tr}^{1/2}} \end{equation} Simplificando: \begin{equation} \frac{dN_{\epsilon_{tr}}}{N}=2\pi \left(\frac{1}{\pi kT}\right)^{3/2}e^{\frac{-\epsilon_{tr}}{kT}\epsilon_{tr}^{1/2}}d\epsilon_{tr} \end{equation} $dN_{\epsilon_{tr}}$ representa el número de moléculas cuya energía traslacional está comprendida entre $\epsilon_{tr}$ y $\epsilon_{tr}+d\epsilon_{tr}$
La energía traslacional media es la misma para todos los gases a la misma temperatura.