En esta sección vamos a deducir la ecuación que nos permite conocer la fracción de moléculas que tienen el módulo de su velocidad comprendida entre dos valores determinados.
Llamamos $dN_v/N$ a la fracción de moléculas con velocidad comprendida entre v y v+dv. Donde N representa el número total de moléculas del gas. \begin{equation} \frac{N_v}{N}=G(v)dv \end{equation} G(v) es la función de distribución de velocidades o densidad de probabilidad. Al multiplicar esta función por $dv$ se obtiene la fracción de moléculas con velocidad comprendida entre v y v+dv.
Si nos interesa calcular la fracción de moléculas con velocidad comprendida entre $v_1$ y $v_2$, integramos la función de distribución de velocidades en ese intervalo. (Es equivalente hablar de fracción de moléculas que tienen su velocidad en un intervalo dado y probabilidad de que una molécula tenga su velocidad comprendida en dicho intervalo) \begin{equation} P[v_1,v_2]=\int_{v_1}^{v_2}G(v)dv \end{equation} La probabilidad de que una molécula tenga su velocidad comprendida en el intervalo $[0,\infty]$ es 1 \begin{equation} \int_{0}^{\infty}G(v)dv=1 \end{equation}
Para obtener G(v) debemos integrar la función $\phi(\vec{v})=g(v_x)g(v_y)g(v_z)$ para un valor v del módulo de velocidad a lo largo del espacio. Dado que esta integral se extiende sobre un casquete esférico es conveniente el uso de coordenadas esféricas ($v,\theta, \varphi$). \begin{equation} g(v_x)g(v_y)g(v_z)dv_xdv_ydv_z=\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^2/2kT}dv_xdv_ydv_z \end{equation} Haciendo el cambio a esféricas, $dv_xdv_ydv_z=v^2sen\theta dvd\theta d\varphi$, e integrando: \begin{equation} \frac{dN_v}{N}=G(v)dv=\int_{0}^{\pi}\int_{0}^{2\pi}\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^2/2kT}v^2sen\theta dvd\theta d\varphi \end{equation} Dado que v y su diferencial son constantes podemos sacarlas fuera de la integral. \begin{equation} \frac{dN_v}{N}=G(v)dv=\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^2/2kT}v^2dv\int_{0}^{\pi}\int_{0}^{2\pi}sen\theta d\theta d\varphi \end{equation} \begin{equation} \frac{dN_v}{N}=G(v)dv=\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^2/2kT}v^2dv4\pi \end{equation} Donde la función de distribución del módulo de la velocidad G(v) es: \begin{equation} G(v)=\left(\frac{m}{2\pi kT}\right)^{3/2}e^{-mv^2/2kT}4\pi v^2 \end{equation} A valores pequeños del módulo de la velocidad predomina el término parabólico ($v^2$) y la función crece cuadráticamente. A valores elevados de v comienza a dominar la exponencial negativa $e^{-v^2}$ haciendo que la función G(v) disminuya su valor, anulándose en el infinito.
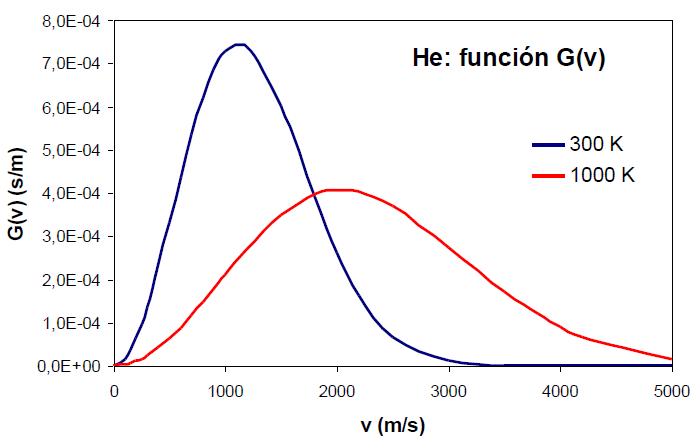
El incremento de la temperatura produce un ensanchamiento en la función de distribución y un desplazamiento de su máximo a velocidades mayores.
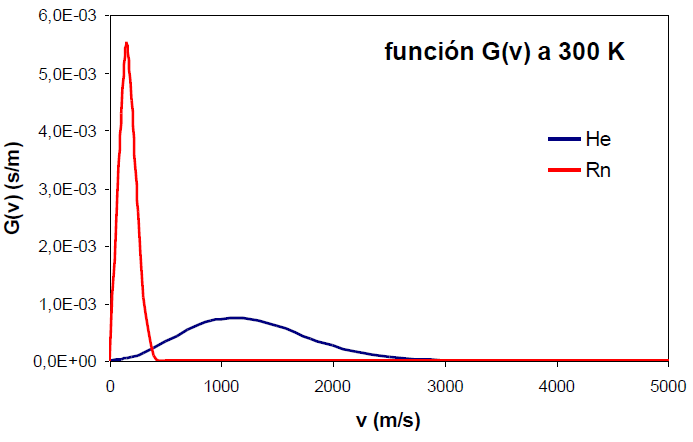
Un incremento en la masa molecular, sin embargo, produce el efecto contrario, estrechamiento de la función y desplazamiento de su máximo a velocidades menores.