La probabilidad de encontrar una molécula en un determinado nivel energético, j, viene dada por:
\begin{equation} p_j=\frac{e^{-\epsilon_j/kT}}{\sum e^{-\epsilon_i/kT}} \end{equation}
Desde el punto de vista clásico la energía cinética de una molécula varía de forma continua y viene dada por la expresión $\epsilon_x=\frac{1}{2}mv_x^2$. Llevando este valor de energía a la expresión de la probabilidad se obtiene:
\begin{equation} dp(v_x)=\frac{dN_{v_x}}{N}=\frac{e^{-\frac{mv_x^2}{2kT}}dv_x}{\int_{-\infty}^{\infty}e^{-\frac{mv_x^2}{2kT}}dv_x} \end{equation}
Donde, $dp(v_x)$ representa la fracción de moléculas con velocidad comprendida entre $v_x$ y $v_x+dv_x$. La integral del denominador representa la suma a lo largo de todos los posibles valores de $v_x$ y tiene la forma $\int e^{-bx}dx=(\pi/b)^{1/2}$
\begin{equation} dp(v_x)=\frac{dN_{v_x}}{N}=\frac{e^{-\frac{mv_x^2}{2kT}}dv_x}{\left(\frac{2\pi kT}{m}\right)^{1/2}} \end{equation}
Teniendo en cuenta que, $\frac{dN_{v_x}}{N}=g(v_x)dv_x$, la función de distribución para $v_x$ viene dada por:
\begin{equation} g(v_x)=\left(\frac{m}{2\pi kT}\right)^{1/2}e^{-mv_{x}^{2}}/2kT \end{equation}
Donde m es la masa de una molécula del gas, k es la constante de Boltzmann y T la temperatura.
Las expresiones para $g(v_y)$ y $g(v_z)$ son análogas dada la equivalencia entre las direcciones espaciales.
\begin{equation} g(v_x)=\left(\frac{m}{2\pi kT}\right)^{1/2}e^{-mv_{y}^{2}}/2kT \end{equation}
\begin{equation} g(v_x)=\left(\frac{m}{2\pi kT}\right)^{1/2}e^{-mv_{z}^{2}}/2kT \end{equation}
Las unidades de la función de distribución son inversas a las de la velocidad, para que la probabilidad obtenida al multiplicarla por $dv_x$ sea adimensional.
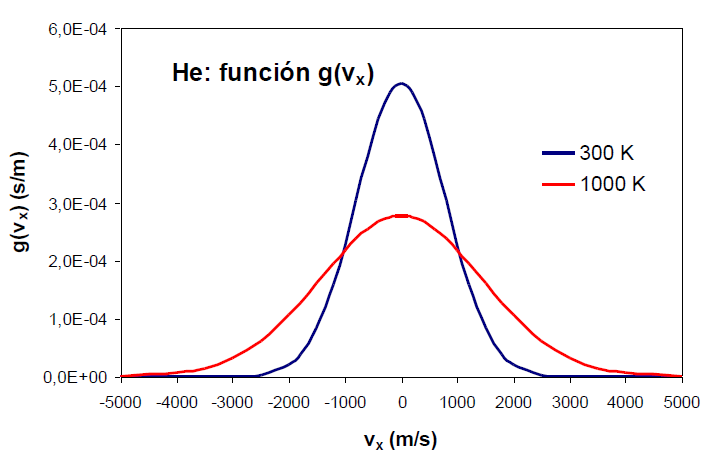
La función $g(v_x)$ es gaussiana, centrada en $v_x=0$ y simétrica respecto al eje de ordeandas (y). Esta simetría hace que la densidad de probabilidad de encontrar moléculas en $v_x=a$ sea igual a la probabilidad de encontrarlas en $v_x=-a$. La densidad de probabilidad alcanza su máximo en cero, tendiendo hacia cero a medida que $v_x$ se va hacia $\pm \infty$.
Un aumento de la temperatura del gas produce un aumento en la densidad de probabilidad para valores altos, tanto positivos como negativos, de la velocidad.
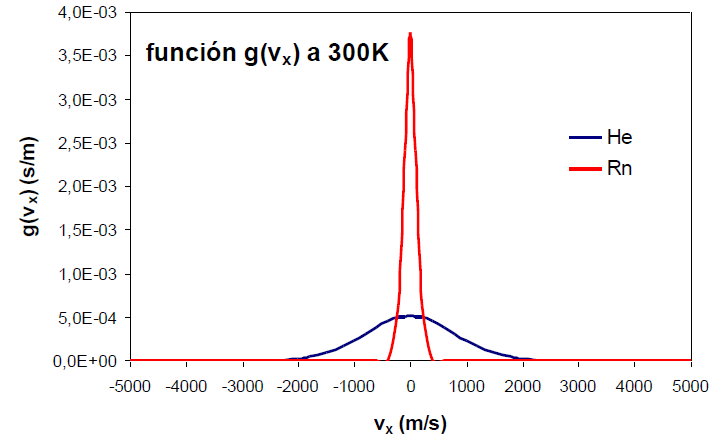
Un efecto similar al de la temperatura podemos observarlo al variar la masa del gas. En la siguiente gráfica se aprecia como al disminuir la masa del gas la función de distribución se ensancha. Por tanto, la masa y la temperatura tienen efectos contrarios en la función de distribución, una disminución de masa o aumento de la temperatura producen el ensanchamiento de la curva.