 Otro fenómeno que la física clásica no podía explicar era la emisión de radiación por parte de un cuerpo negro. Un cuerpo negro es un objeto capaz de absorber toda la radiación que le llega sin reflejar nada. La intensidad de la radiación emitida por un cuerpo negro varía con la longitud de onda según una curva característica que presenta un máximo dependiente de la temperatura del cuerpo. Según la teoría clásica la intensidad de la radiación emitida por el cuerpo negro debe aumentar, según disminuye la longitud de onda, haciéndose infinita, comportamiento que carece de sentido físco.
Otro fenómeno que la física clásica no podía explicar era la emisión de radiación por parte de un cuerpo negro. Un cuerpo negro es un objeto capaz de absorber toda la radiación que le llega sin reflejar nada. La intensidad de la radiación emitida por un cuerpo negro varía con la longitud de onda según una curva característica que presenta un máximo dependiente de la temperatura del cuerpo. Según la teoría clásica la intensidad de la radiación emitida por el cuerpo negro debe aumentar, según disminuye la longitud de onda, haciéndose infinita, comportamiento que carece de sentido físco.
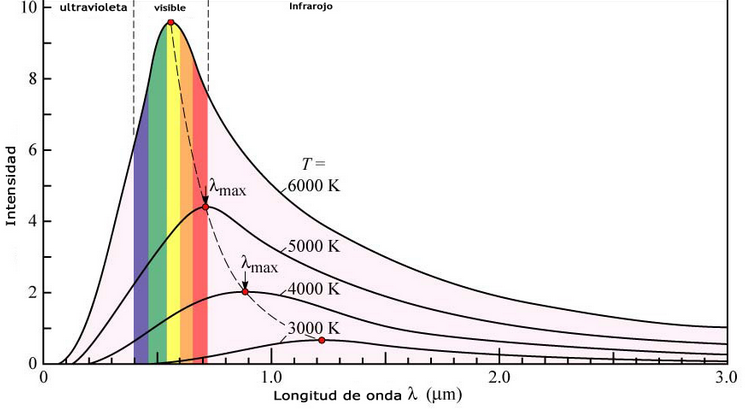
La física clásica intenta predecir estas curvas mediante la ecuación de Rayleigh-Jeans:
$E(\lambda,T)=\frac{2ckT}{\lambda^4}$
Esta ecuación predice bien a longitudes de onda grandes pero falla en la zona ultravioleta, puesto que cuando la longitud de onda tiende a cero la energía radiante tiende a infinito. Problema conocido como la catástrofe ultravioleta.
La longitud de onda a la que las curvas alcanzan su máximo depende de la temperatura. La Ley de Wien predice dicho máximo:
$\lambda_{max}=\frac{0.0028976\;mK}{T}$
Como puede observarse el máximo se alcanza a longitudes de onda menores a medida que aumenta la temperatura.
La solución a este enigma llegó de la mano de Max Planck en 1900. Para explicarlo Planck debe romper con la física clásica y suponer que el cuerpo negro emite radiación en forma de pequeños paquetes, llamados cuantos de energía. La energía de uno de estos paquetes viene dada por la ecuación:
\begin{equation} E=h\nu \end{equation} donde, $h=6.62607x10^{-34}\ Js$. Llamada ecuación de Planck.
Bajo esta suposición, Planck llega a una ecuación que describe a la perfección las curvas de intensidad observadas.
\begin{equation}E(\nu,T)=\frac{8\pi h\nu^3}{c^2}\frac{1}{e^{h\nu/kT-1}}\end{equation}
Llamada Ley de Plack.



