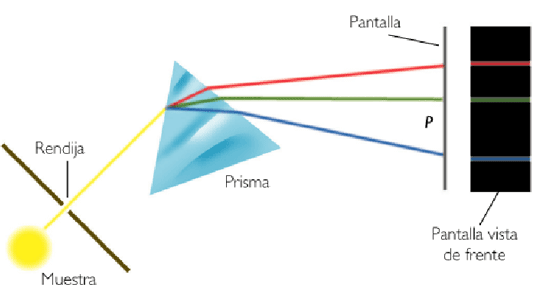
Cuando descomponemos la luz del sol mediante un prisma obtenemos un espectro continuo, formado por un elevado número de longitudes de onda.
Los gases, por el contrario, generan espectros discontinuos o de líneas. En la siguiente figura se muestra el espectro del helio, obtenido al excitar los átomos de helio mediante una descarga eléctrica, energía que absorben para emitirla posteriormente en forma de luz.

La luz emitida por los átomos de helio cuando se desexcitan pasas a través de una rendija, dispersándose en un prisma y siendo registrada mediante una película fotográfica.
Cada elemento químico tiene un espectro característico, que permite identificarlo. Así, el helio (del griego, helios, significa sol) fue descubierto durante un eclipse solar, 27 años antes de ser aislado.
En 1885, Johamm Balmer, obtuvo de forma empírica una ecuación que predecía las frecuencias a las que aparecían las líneas espectrales del átomo de hidrógeno en la región visible (serie de Balmer).
\begin{equation} \nu=3.2881x10^{15}\ s^{-1}\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \end{equation}
Donde, $\nu$, es la frecuencia a la que aparece cada línea del espectro y $n$ un número entero mayor o igual a dos.
Sustituyendo en la ecuación n=3 se obtene la frecuencia de la línea roja, con n=4 la azul verdosa, con n=5 la azul y así sucesivamente.

Las líneas espectrales nos dan una importante información sobre la estructura de los átomos, sugiriendo que los electrones solo pueden encontrarse en ciertos niveles de energía. Estas observaciones experimentales no podían ser explicadas mediante la física clásica, dando lugar al nacimiento de una nueva teoría, la mecánica cuántica.
En 1888, Rydberg propuso una fórmula que generaba las lineas espectrales tanto en la zona visible como en la infrarroja y ultravioleta.
\begin{equation}\nu=3.29x10^{15}\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)\end{equation}
Siendo $n_i$ y $n_f$ números enteros, con $n_i>n_f$
La constante de Rydberg puede expresarse en diferentes unidadades:
$R=1.096x10^{7}\;m^{-1}$
$R=3.29x10^{15}\;s^{-1}$
$R=2.18x10^{-18}\;J$



