La ecuación diferencial (16) tiene una solución del tipo:
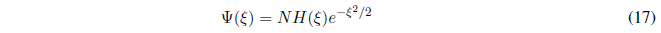
Calculamos las derivadas primera y segunda de (17):
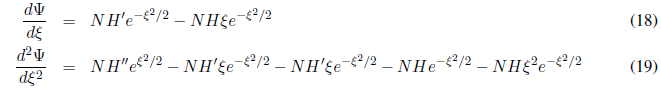
Sustituyendo (17) y (19) en (16) y simplificando
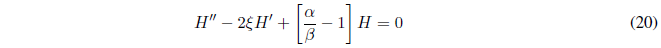
La ecuación (20) es conocida con el nombre de ecuación diferencial de Hermite. H es una función polinómica, conocida como polinomio de Hermite.
El polinomio de Hermite tiene la siguiente forma:
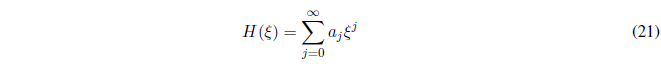
Derivando (21)
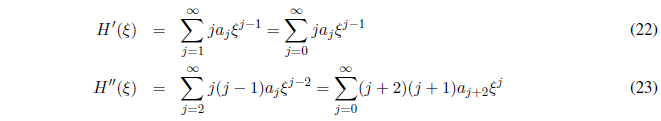
Sustituyendo las ecuaciones (21), (22) y (23) en (20):
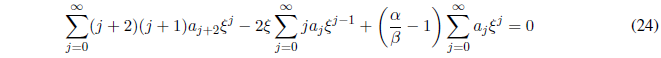
Agrupando todos los términos en un sumatorio y sacando factor común:
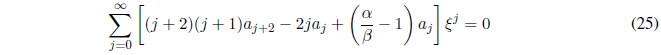
Para que la ecuación (25) se cumpla los términos encerrados entre corchetes deben ser nulos
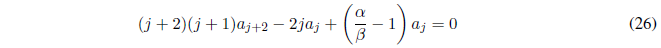
Despejando \(a_{j+2}\) se obtiene la relación de recurrencia.
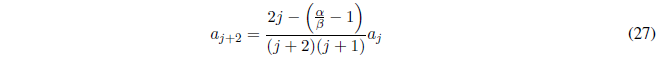
Conocidos los coeficientes \(a_0\) y \(a_1\) del polinomio de Hermite se pueden calcular el resto de coeficientes utilizando la ley de recurrencia.
Para que la función de onda sea válida en Mecánica Cuántica debe ser cuadráticamente integrable, es decir, normalizable.
El polinomio de Hermite es un desarrollo con infinitos términos y crece es más rápido que decrece la exponencial, haciendo que la función de onda tienda a infinito cuando x tiende a más infinito y a menos infinito.
Para que la función de onda se cuadráticamente integrable es necesario truncar el polinomio para un valor de \(j=v\), de manera que \(a_v\) es el último coeficiente no nulo del desarrollo.
Haciendo \(j=v\) en la ley de recurrencia, nos da:
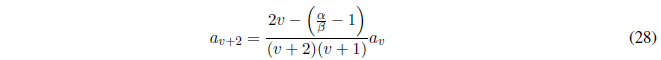
Como \(a_v\) es el último término no nulo y \(a_{v+2}=0\), la ecuación (28) se cumplirá sólo si el numerador del cociente es nulo.
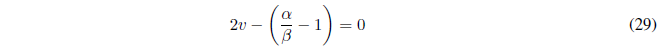
Sustituyendo \(\alpha\) y \(\beta\) por su valor
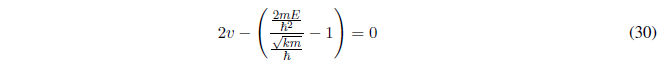
Despejando E en (30) nos queda:
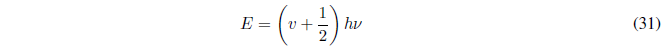
Donde \(\nu\) representa la frecuencia del oscilador y v es el número cuántico que toma valores 0,1,2,3,.....
Características del oscilador armónico unidimensional
- La energía del oscilador armónico está cuantizada de acuerdo con el número cuántico v=1,2,3,....
- El estado v=0, es el de menor energía (estado fundamental)
- Los niveles de energía del oscilador armónico están igualmente espaciados. Al aumentar v en una unidad la energía aumenta en \(h\nu\)



