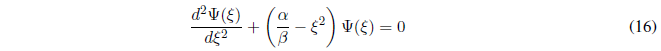Planteamos la ecuación de Schrödinger:
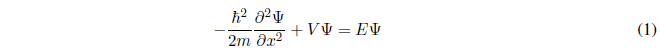
El oscilador armónico está sometido a un potencial del tipo: \(V(x)=\frac{1}{2}kx^2\)
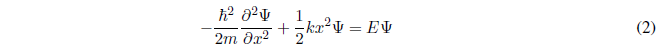
Despejando la derivada de mayor grado, la ecuación (2) puede escribirse:
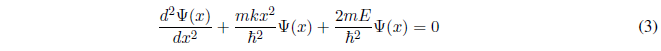
Simplificamos la ecuación (3) definiendo las siguientes magnitudes:
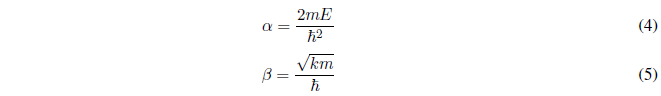
Sustituyendo (4) y (5) en (3):
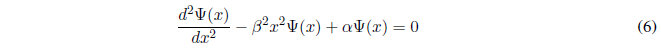
La resolución de la ecuación (6) requiere el siguiente cambio de variable:
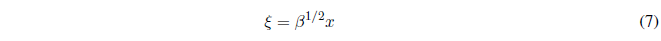
Aplicando la regla de la cadena:
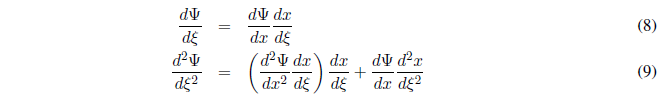
Despejando x de (7) y derivando respecto a \(\xi\) obtenemos:
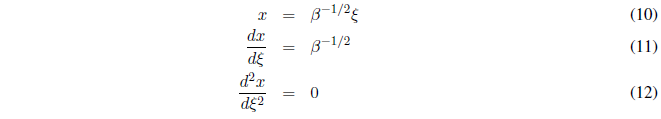
Sustituyendo (11) y (12) en (9) y despejando \(\frac{d^2\Psi}{dx^2}\):
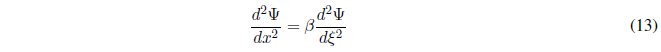
Sustituyendo (10) y (13) en (6):
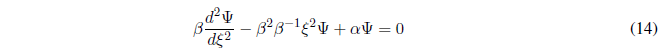
Dividiendo (14) por \(\beta\):
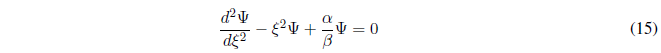
Sacando factor común a la función de onda se obtiene la ecuación de Hermite - Gauss, conocida en Matemáticas incluso antes del nacimiento de la mecánica cuántica.