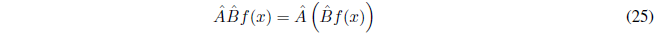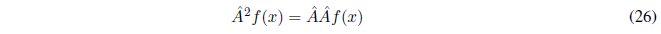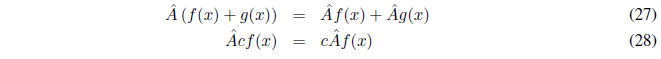An operator acts on a function transforming it into another. Let us take as an example the derivative operator that we represent by \(\hat{D}\), a circumflex is used to indicate that it is an operator, although it can be dispensed with as long as its nature is evident.
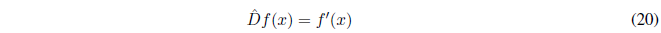
The operator acts on the function f(x) and returns its derivative. Another well-known operator is the integral, the inverse operation of the derivative. But there are also other operators such as:
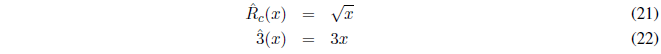
The square root operator takes the square root of the function on which it acts. The operator 3 multiplies by 3.
The sum of two operators \(\hat{A}\) and \(\hat{B}\) is defined by the equation:
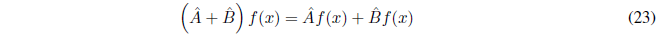
and the difference as:
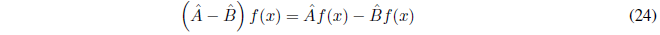
We define the product of the operators \(\hat{A}\) and \(\hat{B}\) as: