We will begin by introducing Postulate I of Quantum Mechanics. However, it should be noted that the number of postulates and their order are not unique, but that there are different sets of them that are physically equivalent.
Postulate I.- The state of a physical system is described by a function \(\Psi (q,t)\) of the coordinates \((q)\) and of time \(t\). This function, called the state function or wave function, contains all the information that can be determined about the system. Furthermore, we postulate that \(\Psi (q,t)\) takes simple values, is finite, continuous, with continuous derivatives and integrable square.
The wave function \(\Psi (q,t)\) must be conceived as a mathematical function that gives us information about the system and from which we can calculate its properties.
What information does the wave function provide? Max Born of the Copenhagen School indicated that the squared modulus of the wave function represents the probability density of finding the system in the state with coordinate \(q\). ![]()
The product of the probability density by a differential element of length \(dq\) gives us the probability that the particle is in a state whose coordinates are between \(q\) and \(q+dq\) at the moment t. ![]()
Consider a particle moving along the x axis. In this case the wave function depends only on x, \(\Psi (x,t)\) we take n identical systems that do not interact with each other and all in the same state defined by \(\Psi (x,t) \). We measure the position of the particle in each of the n systems, therefore, we will obtain n measurements. We will call \(dn_x\) the number of measurements in which the particle's position is between x and x+dx. Then \(dn_{x}/n\) represents the probability that the particle is between x and x+ dx, that is: ![]()
This example allows us to see the connection between probability density and experimental measurements.
We might think that it can be obtained by making multiple measurements on a single system, initially in the state \(\left|\Psi(x,t)\right|^2\), however, the result obtained would not be valid since the process of measurement changes the quantum state of the system.
The probability that the particle is between the points \(x_1\) and \(x_2\) is given by the integral: 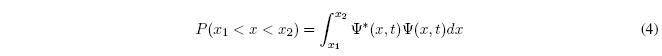
If we extend the integral along the entire x-axis and the result is 1, the wavefunction is said to be normalized.
As we can see, Quantum Mechanics does not allow the exact measurement of the position in which the particle is located. We can only predict the probability of a possible outcome.
The evolution in time of the state of a system in Classical Mechanics is given by Newton's second law. What equation gives us the evolution in time of the wave function in Quantum Mechanics?
Postulate II answers this question.
Postulate II.- The evolution in time of the state of a system is given by the Schrödinger equation dependent on time. 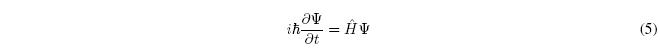
Where \(\hbar=h/2\pi\), where h is a universal constant known as Planck's constant, and where \(\hat{H}\) is the Hamiltonian (or Hamiltonian) operator of the system.
For a single particle moving along the x-axis, \(\hat{H}\) is given by: ![]()
Where m is the mass of the particle and V(x,t) the potential energy to which it is subjected. The Hamiltonian is the operator associated with the energy of the system, therefore, it is logical to think that the first term is the kinetic energy of the system.



