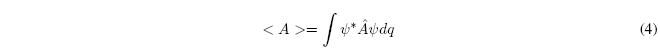Postulate I.- The state of a physical system is described by a function \(\Psi(q,t)\) of the coordinates (q) and time (t). This function, called the state function or wave function, contains all the information that can be determined about the system. In addition, we postulate that \(\Psi(q,t)\) takes simple values, is finite, continuous, with continuous derivatives and integrable square.
Postulate II.- The evolution in time of the state of a system is given by the Schrödinger equation dependent on time:
\begin{equation}i\hbar\frac{\partial\Psi(q,t)}{\partial t}=\hat{H}\Psi(q,t)\end{equation}
Where \(\hbar=\frac{h}{2\pi}\), where h is a universal constant known as Planck's constant, and where \(\hat{H}\) is the Hamiltonian (or Hamiltonian) operator of the system.
For a single particle moving along the x-axis, \(\hat{H}\) is given by:
\begin{equation}\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial}{\partial x}+V(x,t)\end{equation}
Postulate III.- Each physical observable in Quantum Mechanics corresponds to a linear and Hermitian operator. To find such an operator, we write the mechanoclassical expression of the observable in terms of the Cartesian coordinates and the corresponding linear moments. Next, we replace each coordinate \(x\) by the operator \(\hat x\) (multiply by x) and each momentum \(p_x\) by the operator \(-i\hbar\frac{\partial} {\partial x}\).
Postulate IV.- Regardless of the state function of a system, the only values that can result from a measurement of the physical observable A are the eigenvalues a, of the equation: \(\hat{A} f_i = a f_i \)
Postulate V.- If \(\hat{A}\) is a linear Hermitian operator that represents a physical observable, then the eigenfunctions \(\psi_i\) of the eigenvalue equation \(\hat{A}\psi_i =a_i \psi_i\), form a complete set. This means that any state function \(\Psi\) that satisfies the same boundary conditions as each \(\psi_i\) can be expressed as a linear combination of the eigenstates of \(\hat{A}\). ![]()
Postulate VI.- If \(\psi_i(q,t)\) is the normalized state function of a system at time t, then the mean value of a physical observable A at time t is: