Eigenvalue equations are those that have the following form:
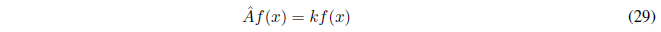
The operator \(\hat{A}\) acts on the function f(x) and generates the function multiplied by a constant k. It is an eigenvalue equation. f(x) is the eigenfunction of the operator \(\hat{A}\) and k is the eigenvalue. Eigenvalue equations are of great importance in Quantum Mechanics since the Schrödinger equation is such an equation.
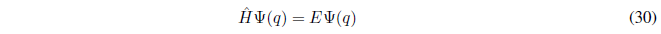
It is simple to show that if a function f(x) is proper to an operator \(\hat{A}\) with eigenvalue k, then all functions of the form cf(x), where c is a constant, are proper to the operator \(\hat{A}\) with eigenvalue k.



