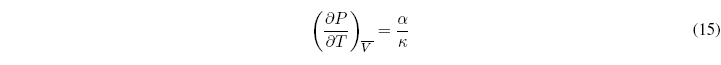The relationship between the state variables of a system (P, V, T, n) is given by an equation called the equation of state.
As an example we have the ideal gas equation of state PV=nRT. Only an ideal gas fulfills this equation of state and, as can be seen, it relates the state variables, so that once three of them are known, the fourth can be obtained.
We can ask ourselves what happens with real gases, are there equations of state for them? The answer is yes, one of the best known equations applicable to real gases is the van der Waals equation which has the following form: 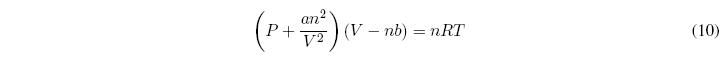
a and b are characteristic constants of each gas. If a and b are zero, the ideal gas equation is obtained. The term nb that subtracts from the volume takes into account the molecular repulsion. The term an 2 /V 2 takes into account the molecular attraction that tends to cause the pressure to be less than that predicted by the ideal gas equation.
There are six very useful partial derivatives in thermodynamics, because they can be measured very easily:
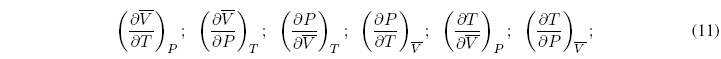
These six relations are not independent since three of them are the inverses of the other three.
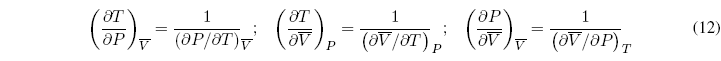
In addition, we can propose one more equation that relates three of the partial derivatives:
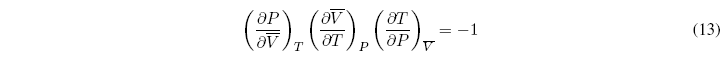
This relationship allows us to clear one of the relationships based on the other two. Therefore only two of the partial derivatives are independent and the remaining four can be calculated from them.
These independent derivatives are known as thermal expansion or coefficient of cubic expansion (\(\alpha\)) and isothermal compressibility (\(\kappa\)).
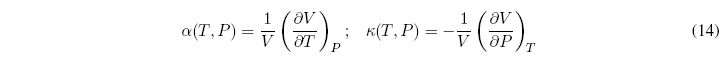
The relationship between both coefficients is given by the expression: