When a thermodynamic system goes from state 1 to state 2, it is said to have undergone a thermodynamic process. The intermediate thermodynamic states that lead from state 1 to 2 are called trajectories or paths. Two processes with different trajectories can connect the same initial and final states.
Let us now study some particular processes:
(a) Cyclic process , the initial and final states are the same. All state functions will be null for this process.
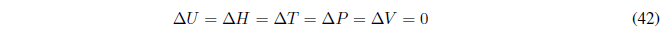
However, \(q\) and \(w\) do not have to be zero for a process of this type since they are not state functions and their value depends on the trajectory that the system follows to go from point 1 to 2. .
(b) Reversible phase change at constant T and P , the heat exchanged is the heat of phase change that can be measured experimentally. The work is calculated with the integral:
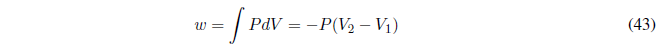
The initial and final volumes can be calculated from the density of the substances or in case of being an ideal gas from the equation of state \(PV=nRT\).
The enthalpy change coincides with the heat exchanged in the phase change, \(\Delta H=q_p\).
The variation of internal energy is calculated with the first principle, \(\Delta U=q_p + w\)
(c) Heating at constant pressure without phase change , we begin by calculating the work, . The exchanged heat coincides with the enthalpy change that can be obtained from the following equation:
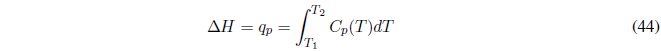
equation valid at constant P.
The change of internal energy is calculated with the first principle: \(\Delta U =q_p +w\)
(d) Heating at constant volume without phase change, given that the volume remains constant \(w = 0\) and the heat is equal to the change in internal energy, which can be calculated with the equation:
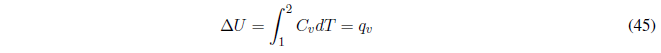
The enthalpy change must be calculated from the internal energy change with the expression, $\Delta H=\Delta U+\Delta(PV)$ , which at constant volume remains: \(\Delta H=\Delta U +V\DeltaP\).
(e) Adiabatic expansion of a perfect gas in a vacuum , in an expansion against a vacuum no work is done \(w=0\). As the process is adiabatic there is no heat exchange \(q=0\). By the first principle the variation of internal energy is also zero. The calculation of the enthalpy change can be done with the equation, \(\Delta H=\Delta U +P\Delta (PV)= \Delta U +nR\Delta T=0\). In this process there can be no change in temperature since it would mean a change in the internal energy of the gas.



