For a first order reaction $aA \rightarrow P$, we write, \begin{equation} \frac{d[A]}{dt}=-k_A[A] \end{equation} This differential equation is very easy to solve , but suppose that we do not know its solution. Euler's method consists of approximating, for a small interval of time, the differentials by increments. \begin{equation} \frac{\Delta [A]}{\Delta t}=-k_A[A]\;\;\;\; \Rightarrow \Delta [A]=-k_A[A]\Delta t \end{equation} Substituting the increments for two concentrations close in time $[A]_n$ at time $t$ and $[A]_{n +1}$ to time $t_{n+1}$, gives us: \begin{equation} [A]_{n+1}-[A]_{n}=-k_A(t_{n+1} -t_n) \end{equation} This last equation represents the tangent line to the curve of [A] vs t at the point $[A]_n, t_n$.
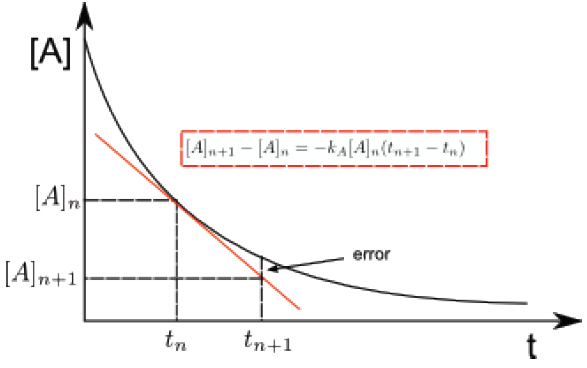
Let's see an example: Calculate [A] for t = 1s, if $[A]_0= 1\; mol/l$ and $k=10^{-3}s^{-1}$, we assume first-order kinetics. Applying equation (3). $[A] - 1 = -10^{-3}(1 - 0)$, therefore $[A] = (1-10^{-3})\; mol/l$
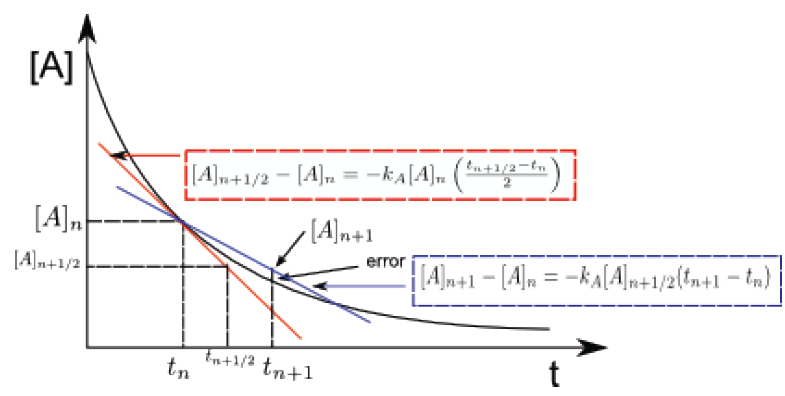
Modified Euler's method (slope at midpoint)
Given $[A]_n$ at time $t_n$, it allows us to calculate $[A]_{n+1}$ at time $t_{n+1}$ using the tangent line that passes through the midpoint of the interval. \begin{equation} [A]_{n+1}-[A]_n=-k_A[A]_{n+1/2}(t_{n+1}-t_n) \end{equation} $[ A]_{n+1/2}$ is obtained with the following equation: \begin{equation} [A]_{n+1/2}-[A]_n=k_A[A]_n\left(\frac {t_{n+1}-t_n}{2}\right) \end{equation} Equation (5) calculates the value of [A] at the midpoint of the interval, using $t_{n+1/ 2}$, which is the time in the middle of the interval. Once $[A]_{n+1/2}$ has been calculated, it is substituted in (4) obtaining the concentration $[A]_{n+1}$
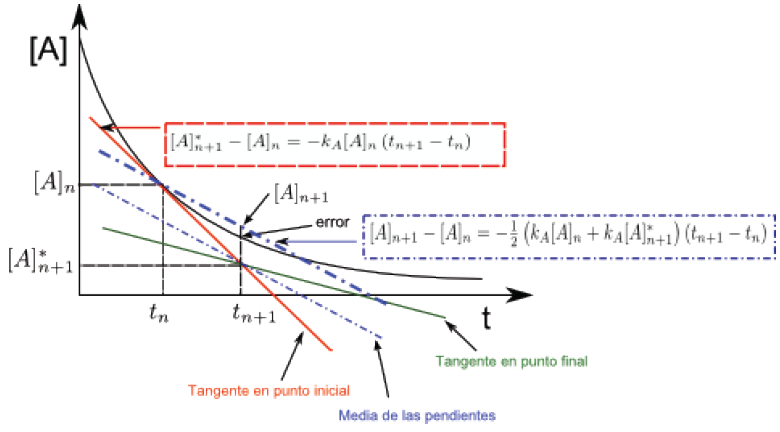
Improved Euler's method (mean of the slopes
Knowing an initial concentration $[A]_n$ at time $t_n$, the concentration $[A]_{n+1}$ at time $t_{n+1}$ is calculated, using a straight line whose slope is average of the slopes of the tangent lines to the curve [A] vs t at the points $[A]_n$ and $[A]_{n+1}$.\\ The equations that allow the calculation for a kinetics of first order are: \begin{equation} [A]_{n+1}-[A]_{n} = -\frac{1}{2}\left(k_{A}[A]_{ n}+k_{A}[A]_{n+1}^{\ast}\right)(t_{n+1}-t_n) \end{equation} $[A]_{n+1}^ {\ast}$ is obtained with the equation: \begin{equation} [A]_{n+1}^{\ast}-[A]_{n} = -k_{A}[A]_{n }\left(t_{n+1}-t_{n}\right) \end{equation} With equation (7) we calculate the concentration of A, at time $t_{n+1}$. Substituting this concentration in (6) $[A]_{n+1}$ is obtained, given by the line whose slope is the mean of the slopes of the lines tangent to the curve at the ends of the interval.