The major steps of the $2H_2+O_2 \rightarrow H_2O$ reaction are believed to correspond to a branched chain reaction, with elementary steps: \begin{eqnarray} H_2 & \rightarrow & 2H\\ H_2+OH & \rightarrow & H + H_2O\\ H + O_2 & \rightarrow & OH + O\\ O + H_2 & \rightarrow & OH + H\\ 2H + wall & \rightarrow & H_2\\ H+O_2+M & \rightarrow & HO_2 + M^{\ast} \end{eqnarray} The $HO_2$ radical is long-lived, and the O and OH radicals are much more reactive than H.
1. Identify the stages of initiation, propagation, branching, and termination.
2. Show that, from the balance of the propagation and branching stages, the result is the overall reaction plus net radical generation.
3. Apply the steady state hypothesis to the concentrations of the free radicals O and OH to find their concentrations as a function of that of H (more abundant).
4. Considering that stage 5 is of order 1 (controlled by adsorption and diffusion on the walls) and stage 1 is of order zero (produced at a constant rate by external circumstances), find the differential equation that governs the generation of radicals h.
5. The solution of the differential equation has two regimes, depending on the sign of b. Discuss the conditions under which each of these regimes occurs, and their meaning.
Solution
1. The branched chain radical reaction consists of four stages.
- In the initiation (1) radicals are generated that pass to the propagation stage.
- In the propagation step (2) the reaction product is generated.
- In the two stages of branching (3)(4) one radical gives rise to two radicals, which produces an acceleration of the reaction that can lead to an explosion.
- In the termination stages (5)(6) the radicals unite with each other, due to the disappearance of the reactants.
2. As can be seen, the sum of the stages of propagation and termination produces a net generation of radicals. \begin{eqnarray} H_2+OH & \rightarrow & H + H_2O\\ H + O_2 & \rightarrow & OH + O\\ O + H_2 & \rightarrow & OH + H\\ -------& - & ------\\ 2H_2+O_2 & \rightarrow & H_2O + OH + H \end{eqnarray}
3. We write the mechanism specifying the kinetic constants of the different stages: \begin{eqnarray} H_2 & \stackrel{k_0}{\rightarrow} & 2H\\ H_2+OH & \stackrel{k_1}{\rightarrow} & H + H_2O\\ H + O_2 & \stackrel{k_2}{\rightarrow} & OH + O\\ O + H_2 & \stackrel{k_3}{\rightarrow} & OH + H\\ 2H + wall & \stackrel{k_4} {\rightarrow} & H_2\\ H+O_2+M & \stackrel{k_5}{\rightarrow} & HO_2 + M^{\ast} \end{eqnarray} We apply the steady state approximation for O radicals. \begin {equation} \frac{d[O]}{dt}=0=k_2[H][O_2]-k_3[O][H_2] \end{equation} \begin{equation} [O]_{ee}= \frac{k_2[H][O_2]}{k_3[H_2]} \end{equation} Now we apply the steady state approximation to OH radicals \begin{equation} \frac{d[OH]}{dt}= 0=-k_1[H_2][OH]+k_2[H][O_2]+k_3[O][H_2] \end{equation} Substituting into the last term of (20) equation (18), gives us: \ begin{equation} \frac{d[OH]}{dt}=0=-k_1[H_2][OH]+\underbrace{k_2[H][O_2]+k_2[H][O_2]}_{2k_2[ H][O_2]} \end{equation} Solving for the OH ntration \begin{equation} [OH]_{ee}=\frac{2k_2[H][O_2]}{k_1[H_2]} \end{equation}
4. We calculate the net variation of radicals H in time, considering that the first stage is of order zero and the fifth of order one. \begin{equation} \frac{d[H]}{dt}=k_0[H_2]^{0}+k_1[H_2][OH]-k_2[H][O_2]+k_3[O][H_2]- k_4[H]-k_5[H][O_2][M] \end{equation} Equation (23) is simplified if we consider equation (18) \begin{equation} \frac{d[H]}{dt} =k_0+k_1[H_2][OH]-k_4[H]-k_5[H][O_2][M] \end{equation} Equation (21) allows the second term of equation (24) to be replaced by $2k_2 [H][O_2]$. \begin{equation} \frac{d[H]}{dt}=k_0+2k_2[H][O_2]-k_4[H]-k_5[H][O_2][M] \end{equation} We take out common factor to [H] in (1.10) \begin{equation} \frac{d[H]}{dt}=k_0+\left(2k_2[O_2]-k_4-k_5[O_2][M]\right)[H] \ end{equation} Calling $f=2k_2[O_2]$ and $g=k_4+k_5[O_2][M]$, the above equation becomes: \begin{equation} \frac{d[H]}{dt }=k_0+(fg)[H] \end{equation}
5. Solving the differential equation gives the following result: \begin{equation} [H]=\frac{k_0}{fg}\left(e^{(fg)t}-1\right) \end{equation} We discuss this solution based on the difference $fg$.
- If g>f, fg<0, the termination stages predominate over the branching stages and the increase in [H] slows as time passes.
- If f>g, fg> 0, the branching stages predominate over the termination stages and [H] grows exponentially with time. The exponential increase in the number of radicals produces the branching explosion.
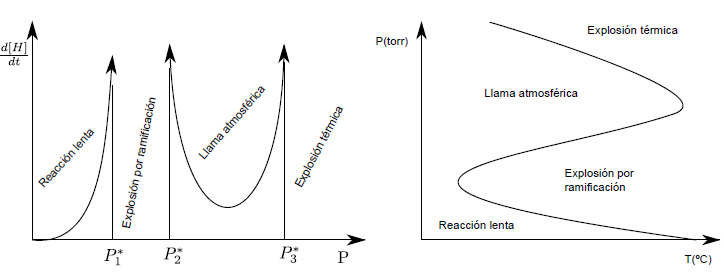
The reaction of hydrogen with oxygen has a pressure-dependent behavior. Thus, at pressures less than $P1^{\ast}$ the reaction is slow. Between $P_{1}^{\ast}$ and $P_{2}^{\ast}$ the explosion is produced, due to the branching that causes an exponential growth of the radicals H. Between $P_{2}^ {\ast}$ and $P_{3}^{\ast}$ a rapid combustion is produced, with a very bright flame, called atmospheric flame. Above $P3^{\ast}$, thermal explosions occur due to the heat released by the reaction, which produces an increase in temperature, with a corresponding increase in the reaction rate.



