Rapid flow method
Many reactions are too fast to be studied by classical methods. Fast flow methods can be used for your study.
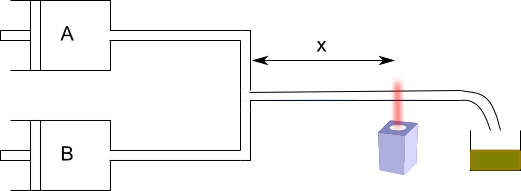
This system allows to measure [A] for small times. The fast flow method allows to study reactions with half-lives between 10 and 10 -3 seconds. The major limitation of fast flow techniques is the mixing time of the reagents. The most effective methods to determine these kinetics are the relaxation methods. In them, a reactive system in equilibrium is started, some variable is changed abruptly (T, P, ect.) and the return of the system to the new equilibrium is studied, being able to determine the kinetic constants.
Relaxation kinetics
Let the elementary reaction be $A\rightleftharpoons B$ , in equilibrium. We introduce a disturbance that changes the equilibrium constant, the system relaxes and reaches a new equilibrium position. Said disturbance may consist of a sudden change in pressure or temperature. At any instant after the perturbation, the concentration of reactant A is given by:
\begin{equation} \frac{d[A]}{dt}=-k_d[A]+k_i[B]\label{ec201} \end{equation}
A time the system reaches the new equilibrium:
\begin{equation} \frac{d[A]}{dt}=0=-k_d[A]_{eq}+k_i[B]_{eq}\label{ec202} \end{equation}
Where, $[A]_{eq}$ and $[B]_{eq}$ are the concentrations of A and B once the new equilibrium has been reached. Let [A] and [B] be the concentrations of A and B at any instant after the disturbance. The relationship between these concentrations, the equilibrium concentrations, and the conversion, x, are given by the following equations:
\begin{equation} [A]_{eq}=[A]-x \;\;\;\; \Rightarrow \;\;\; [A]=[A]_{eq} +x \;\;\; \Rightarrow \;\;\; \frac{d[A]}{dt}=\frac{dx}{dt}\label{ec203} \end{equation} \begin{equation} [B]_{eq}=[B]+x\;\;\; \Rightarrow \;\;\; [B]=[B]_{eq} -x\label{ec204} \end{equation}
Substituting $(\ref{ec203})$ and $(\ref{ec204})$ into $(\ref{ec201})$ we get:
\begin{equation} \frac{dx}{dt}=-k_d( [A]_{eq}-x)+k_i([B]_{eq}-x)\label{ec205} \end{equation}
Simplifying equation $(\ref{ec205})$ with $(\ref{ec202})$ gives:
\begin{equation} \frac{dx }{dt}=-(k_d+k_i)x \end{equation}
Where the sum $k_d+k_i$ is defined as the inverse of the relaxation time,
\begin{equation} \frac{1}{\tau}= k_d+k_i \end{equation}
\begin{equation} \frac{dx}{dt}=\frac{-x}{\tau} \end{equation}
Integrating the last equation gives us the value of x for every instant of time between the disturbance and the new equilibrium.
\begin{equation} \int_{x_0}^{x}\frac{dx}{x}=-\int_{0}^{t}\frac{dt}{\tau}\;\;\;\Rightarrow \;\;\;\; ln\frac{x}{x_0}=-\frac{t}{\tau}\;\;\; \Rightarrow \;\;\; x=x_0e^{-t/\tau} \end{equation}
Having evaluated the relaxation time and the equilibrium concentrations, the kinetic constants, $k_d$ and $k_i$ can be calculated using equations (2) and (7 )



