El modelo atómico de Rutherford, estudiado en una sección anterior, no explica cómo se distribuyen los electrones en el átomo. Además, según la física clásica una partícula cargada y en movimiento -los electrones- emite radiación electromagnética, perdiendo su energía y terminando por caer sobre el núcleo.
El modelo atómico de Bohr resuelve estos problemas basándose en la hipótesis de Planck de la cuantización de la energía.
El modelo de Bohr se fundamenta en los siguientes postulados:
- El electrón se mueve en torno al núcleo en órbitas circulares.
- Las orbitas permitidas para el electrón, en las que no emite energía, son aquellas en las que el momento angular toma valores $n\hbar$, donde n es un número entero. La primera órbita del electrón tiene n=1, la segunda n=2, etc.
- El electrón pasa de unas orbitas a otras mediante la absorción o emisión de cuantos de energía.
Bajo estas suposiciones el modelo de Bohr permite el cálculo de la energía del electrón y del radio de las diferentes órbitas que dependerá del número cuántico n.
Las órbitas permitidas (estados estacionarios) tienen un radio que viene dado por:
\begin{equation} r_n=n^2a_0 \end{equation} donde n=1,2,3,.... y $a_0=0.53\;Anstrong$
La energía del electrón viene dada por:
\begin{equation} E_n=-\frac{R_H}{n^2} \end{equation}
con $R_H=2.179x10^{-18}\ J$
En el estado de más baja energía, n=1, se conoce como estado fundamental. Al aportar energía, el electrón sube a niveles superiores n=2,3,4..... pasando a un estado excitado. Cuando el electrón regresa desde un estado excitado al fundamental emite luz (fotones) cuya energía es igual a la diferencia de energía entre las orbitas final e inicial.
\begin{equation} \Delta E=E_f-E_i=\frac{-R_H}{n_f^2}-\frac{-R_H}{n_i^2}=R_H\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right) \end{equation} Donde, $R_H=2.179x10^{-18}J$
Esta diferencia de energía entre niveles es igual a la energía que posee el fotón emitido o absorbido durante la transición. Por tanto, podemos calcular la frecuencia de dicho fotón con la ecución de Planck.
\begin{equation} \Delta E=h\nu \end{equation}
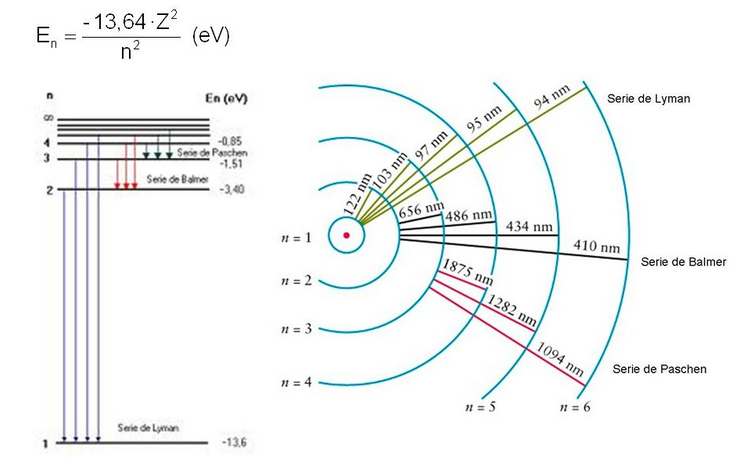
Ejemplo. Determine la longitud de onda de la línea de la serie Balmer del hidrógeno correspondiente a la transición desde n=5 a n=2.
Pasos a seguir: (1) determinar la diferencia de energía entre ambos niveles; (2) igualar esta diferencia de energía a $h\nu$ (energía del fotón emitido; (3) obtener la longitud de onda con la relación $\lambda=c/\nu$.
\begin{equation} \Delta E=2.179x10^{-18}J\left(\frac{1}{5^2}-\frac{1}{2^2}\right)=-4.567x10^{-19}J \end{equation}
El signo menos indica que es energía emitida, ya que el electrón pasa de una orbita superior a otra inferior.
\begin{equation} \nu=\frac{\Delta E}{h}=\frac{4.576x10^{-19}J}{6.626x10^{-34}Js}=6.906x10^{14}s^{-1} \end{equation}
\begin{equation} \lambda=\frac{c}{\nu}=\frac{2.998x10^8\ m/s}{6.906x10^{14}\ s^{-1}}=4.341x10^{-7}\ m \end{equation}
Como podemos ver en este ejemplo el modelo de Bohr permite predecir las líneas espectrales del átomo de hidrógeno. Después de ser excitado, el átomo de hidrógeno, decae emitiendo luz con una frecuencia predecible por este modelo. Sin embargo, el modelo de Bohr fracasa cuando se aplica a átomos con más de un electrón.
Otro logro de la teoría de Bohr es la predicción de la energía de ionización del átomo de hidrógeno que puede generalizarse a cualquier átomo de un sólo electrón. La ionización del átomo consiste en el paso del electrón desde el estado fundamental $(n_i=1)$ hasta el continuo $(n_f=\infty)$
\begin{equation} \Delta E=R_H\left(\frac{1}{1^2}-\frac{1}{\infty}\right)=R_H \end{equation}
El modelo de Bohr tambien funciona con átomo hidrogenoides, que son los que poseen un sólo electrón, aunque su núcleo está formado por más de un protón ($He^+, Li^{2+}$). En este caso la energía de los niveles viene dada por:
\begin{equation} E_n=-\frac{Z^2R_H}{n^2} \end{equation}
Ejemplo. Determinar la longitud de onda de la luz emitida en la transición electrónica desde n=5 a n=3 en el $Be^{3+}$
Restando la energía del nivel final menos la del inicial se obtiene:
\begin{equation} \Delta E=Z^2R_H\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)=4^2\cdot 2.179x10^{-18}J\left(\frac{1}{5^2}-\frac{1}{3^2}\right)=-2.479x10^{-18}\ J \end{equation}
Según la ecuación de Planck $\Delta E=h\nu$ y como $\nu=c/\lambda$, se puede escribir $\lambda=hc/\Delta E$. De donde se obtiene $\lambda=8.013x10^{-8}\ m$.



