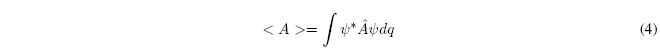Postulado I.- El estado de un sistema físico está descrito por una función \(\Psi(q,t)\) de las coordenadas (q) y del tiempo (t). Esta función, llamada función de estado o función de onda, contiene toda la información que es posible determinar acerca del sistema. Además, postulamos que \(\Psi(q,t)\) toma valores simples, es finita, continua, con derivadas continuas y de cuadrado integrable.
Postulado II.- La evolución en el tiempo del estado de un sistema está dada por la ecuación de Schrödinger dependiente del tiempo:
\begin{equation}i\hbar\frac{\partial\Psi(q,t)}{\partial t}=\hat{H}\Psi(q,t)\end{equation}
Donde \(\hbar=\frac{h}{2\pi}\), siendo h una constante universal conocida como constante de Planck, y donde \(\hat{H}\) es el operador de Hamilton (o Hamiltoniano) del sistema.
Para una única partícula moviéndose a lo largo del eje x, \(\hat{H}\) viene dado por:
\begin{equation}\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial}{\partial x}+V(x,t)\end{equation}
Postulado III.- A cada observable físico en Mecánica Cuántica le corresponde un operador lineal y hermítico. Para encontrar dicho operador, escribimos la expresión mecanoclásica del observable en términos de las coordenadas cartesianas y de los momentos lineales correspondientes. A continuación, reemplazamos cada coordenada \(x\) por el operador \(\hat x\) (multiplica por x) y cada momento lineal \(p_x\) por el operador \(-i\hbar\frac{\partial}{\partial x}\).
Postulado IV.- Independientemente de cuál sea la función de estado de un sistema, los únicos valores que pueden resultar de una medida del observable físico A son los valores propios a, de la ecuación: \(\hat{A} f_i = a f_i\)
Postulado V.- Si \(\hat{A}\) es un operador hermítico lineal que representa un observable físico, entonces las funciones propias \(\psi_i\) de la ecuación de valores propios \(\hat{A}\psi_i =a_i \psi_i\), forman un conjunto completo. Esto quiere decir que cualquier función de estado \(\Psi\) que satisfaga las mismas condiciones límite que cada \(\psi_i\) puede expresarse como combinación lineal de los estados propios de \(\hat{A}\).![]()
Postulado VI.- Si \(\psi_i(q,t)\) es la función de estado normalizada de un sistema al tiempo t, entonces el valor medio de un observable físico A en el instante t es: