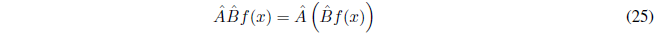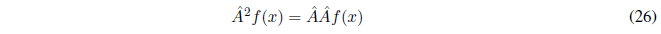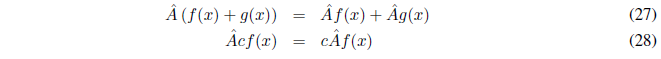Un operador actúa sobre una función transformándola en otra. Pongamos como ejemplo el operador derivada que representamos por \(\hat{D}\), se emplea un circunflejo para indicar que se trata de un operador, aunque se puede prescindir del mismo siempre que sea evidente el carácter de tal.
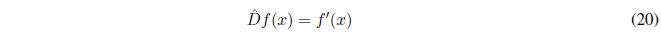
El operador actúa sobre la función f(x) y devuelve su derivada. Otro operador muy conocido es la integral, operación inversa a la derivada. Pero también existen otros operadores como pueden ser:
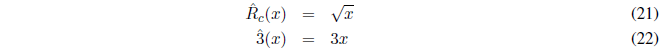
El operador raíz cuadrada hace la raíz cuadrada de la función sobre la que actúa. El operador 3 multiplica por 3.
Se define la suma de dos operadores \(\hat{A}\) y \(\hat{B}\) mediante la ecuación:
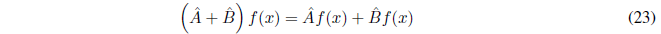
y la diferencia como:
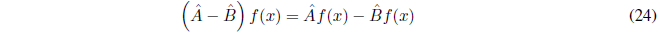
Definimos el producto de los operadores \(\hat{A}\) y \(\hat{B}\) como: