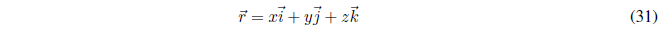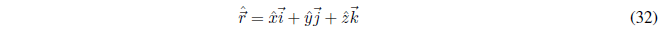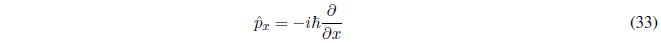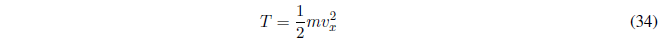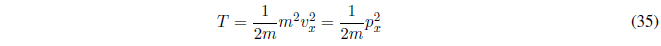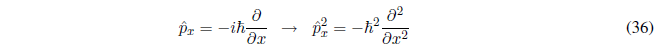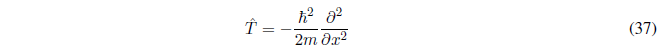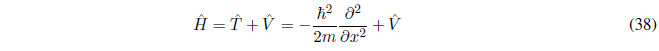Postulado III.- A cada observable físico en Mecánica Cuántica le corresponde un operador lineal y hermítico. Para encontrar dicho operador, escribimos la expresión mecanoclásica del observable en términos de las coordenadas cartesianas y de los momentos lineales correspondientes. A continuación, reemplazamos cada coordenada x por el operador $\hat{x}$ (multiplica por x) y cada momento lineal \(p_x\) por el operador \(-i\hbar\frac{\partial}{\partial x}\).
Veamos como funciona este postulado en la construcción de los operadores más importantes de la Mecánica Cuántica.
Operador posición de una partícula
En Mecánica Clásica la posición de una partícula que se mueve en una dimensión viene dada por la coordenada cartesiana x. La obtención del operador posición consiste en cambiar la coordenada cartesiana x por el operador \(x\). Este operador multiplica por x a la función sobre la que actúa.
Si trabajamos en el espacio tridimensional, la posición de la partícula viene dada por el vector posición:
La obtención del operador posición consiste en el cambio de las coordenadas x,y,z por los respectivos operadores.
Operador momento lineal de una partícula.
En Mecánica Clásica el momento lineal viene dado por el producto de la masa por la velocidad de la partícula.
En Mecánica Cuántica el operador momento lineal está definido en el Postulado III.
Operador energía cinética de una partícula
En Mecánica Clásica la energía cinética viene dada por la siguiente expresión:
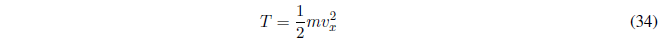
Escribimos esta ecuación en términos del momento lineal \(p_x = mv_x\).
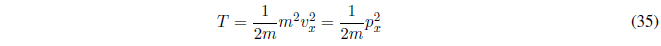
Sustituyendo la cantidad de movimiento por:
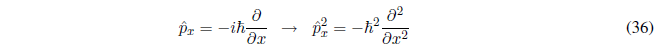
Se obtiene el operador mecanocuántico energía cinética
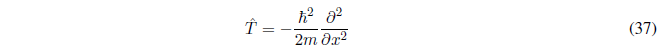
Operador hamiltoniano
Es el operador energía total de una partícula. El hamiltoniano es la suma de las energías cinética y potencial de la partícula.