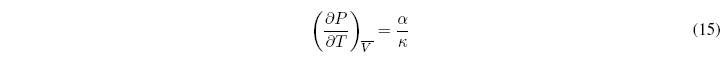La relación entre las variables de estado de un sistema (P, V, T, n) viene dada por una ecuación llamada ecuación de estado.
Como ejemplo tenemos la ecuación de estado del gas ideal PV=nRT. Sólo un gas ideal cumple esta ecuación de estado y como puede observarse relaciona las variables de estado, de modo que conocidas tres de ellas se puede obtener la cuarta.
Podemos preguntarnos que ocurre con los gases reales, ¿existen ecuaciones de estado para ellos?. La respuesta es si, una de las ecuaciones más conocidas aplicables a gases reales es la ecuación de van der Waals que tiene la siguiente forma: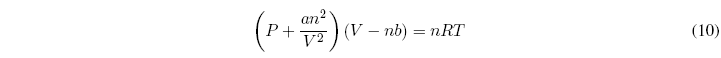
a y b son constantes características de cada gas. Si a y b son cero se obtiene la ecuación del gas ideal. El término nb que resta al volumen tiene en cuenta la repulsión molecular. El término an2/V2 tiene en cuenta la atracción molecular que tiende a hacer que la presión sea inferior a la predicha por la ecuación del gas ideal.
Existen seis derivadas parciales de gran utilidad en termodinámica, porque pueden medirse muy fácilmente:
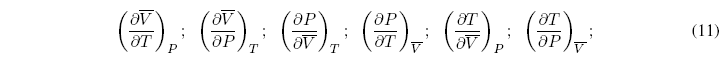
Estas seis relaciones no son independientes ya que tres de ellas son las inversas de las otras tres.
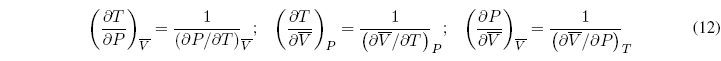
Además podemos plantear una ecuación más que relaciona tres de las derivadas parciales:
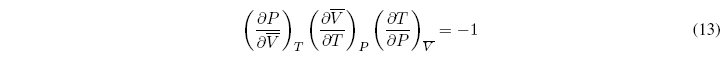
Esta relación nos permite despejar una de las relaciones en función de las otras dos. Por tanto solo dos de las derivadas parciales son independientes y las cuatro restantes pueden calcularse a partir de ellas.
Estas derivadas independientes se conocen como dilatación térmica o coeficiente de dilatación cúbica (\(\alpha\)) y compresibilidad isotérmica (\(\kappa\)).
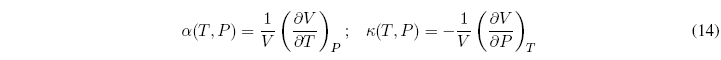
La relación entre ambos coeficientes viene dada por la expresión: