La teoría cinética permite calcular la frecuencia de colisiones entre moléculas. Suponemos que las moléculas son esferas rígidas de diámetro d y despreciamos las fuerzas intermoleculares excepto en el momento de la colisión. A presiones elevadas las fuerzas intermoleculares no pueden ser despreciadas y las ecuaciones obtenidas no son aplicables. Utilizaremos la siguiente notación:
- $z_{12}$: número de colisiones por unidad de tiempo (frecuencia de colisiones) que una molécula del gas 1 experimenta con las moléculas del gas 2.
- $z_{11}$: frecuencia de colisiones que una molécula del gas 1 experimenta con otras moléculas del gas 1.
- $Z_{12}$: frecuencia total de colisiones entre moléculas del gas 1 con las del gas 2 por unidad de volumen.
Sean $N_1$ moléculas del gas 1 con diámetro $d_1$ y $N_2$ moléculas del gas 2 con diámetro $d_2$. Las moléculas se mueven a velocidades medias $\bar{v}_1$ y $\bar{v}_2$.
Comenzamos calculando las colisiones de las moléculas tipo 1 con las tipo 2 $(z_{12})$. Consideremos las moléculas de tipo 2 en reposo y las de tipo 1 moviéndose a velocidad $\bar{v}_{12}$, velocidad media relativa de las moléculas tipo 1 respecto a las tipo 2.
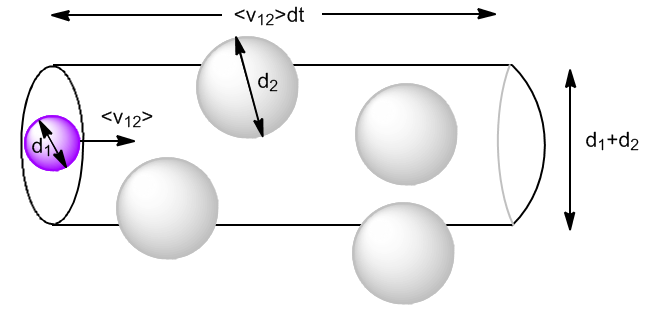
En un dt la molécula 1 reacorrerá una distancia $\bar{v}_{12}dt$ y chocará contra todas las moléculas 2 que se encuentren en el interior de un cilindro de diámetro $d_1+d_2$. El volumen del ciclindro es: \begin{equation} V_{cil}\frac{N_2}{V}=\pi\left(\frac{d_1+d_2}{2}\right)^2\bar{v}_{12}dt\frac{N_2}{V}=\pi d_{12}^{2}\bar{v}_{12}dt\frac{N_2}{V} \end{equation} Siendo $d_{12}$ el diámetro de colisión. También podemos definir una sección eficaz, $\sigma_{12}=\pi d_{12}^2$.
Las colisiones que sufre una partícula de tipo 1 con las de tipo 2 por unidad de tiempo, llamada frecuencia de colisión $z_{12}$ nos queda: \begin{equation} z_{12}=\sigma_{12}\bar{v}_{12}\frac{N_2}{N} \end{equation} Tan solo nos falta obtener el módulo de la velocidad relativa media, $v_{12}>$. considerando colisiones a 90º (media entre 0º y 180º) $\bar{v}_{12}^2=\bar{v}_1^2+\bar{v}_2^2$. Dado que $\bar{v}=\sqrt{\frac{8RT}{\pi M}}$
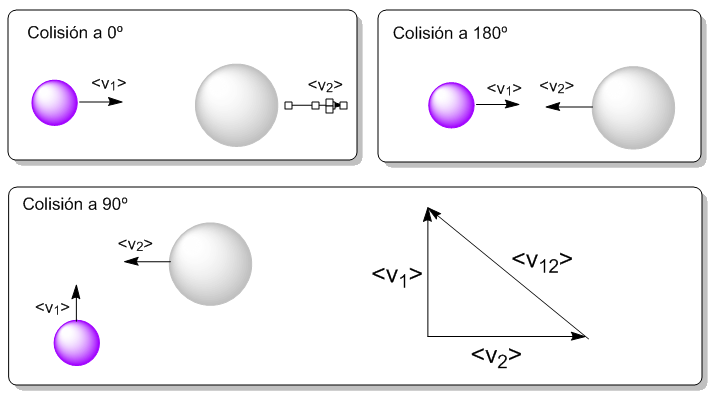
\begin{equation} \bar{v}_{12}^2=\frac{8RT}{\pi M_1}+\frac{8RT}{\pi M_2} \end{equation} Sustituyendo en $z_{12}$ \begin{equation} z_{12}=\sigma_{12}\left[\frac{8RT}{\pi}\left(\frac{1}{M_1}+\frac{1}{M_2}\right)\right]^{1/2}\frac{N_2}{V} \end{equation} Definimos la frecuencia total de colisiones de las moléculas tipo 1 con las tipo 2 como: $Z{12}=z_{12}\cdot N_1$. Dado que es un número muy grande se suele tomar por unidad de volumen: \begin{equation} Z_{12}=z_{12}\frac{N_1}{V} \end{equation} Sustituyendo $z_{12}$ \begin{equation} Z_{12}=\sigma_{12}\left[\frac{8RT}{\pi}\left(\frac{1}{M_1}+\frac{1}{M_2}\right)\right]^{1/2}\frac{N_1}{V}\frac{N_1}{V} \end{equation} En general $z_{12}\neq z_{21}$ pero $Z_{12}=Z_{21}$
Las colisiones entre moléculas de tipo 1 son: \begin{equation} z_{11}=\pi d_{11}^2<v_{11}>\frac{N_1}{V} \end{equation} donde \begin{equation} d_{11}=\frac{d_1+d_1}{2}=d_1 \end{equation} \begin{equation} \bar{v}_{11}^2 =\bar{v}_1^2+\bar{v}_1^2=2\bar{v}_1^2=2\frac{8kT}{\pi m} \end{equation} Sustituyendo \begin{equation} z_{11}=\sqrt{2}\pi d_1^2\left(\frac{8kT}{\pi m}\right)^{1/2}\frac{N_1}{V} \end{equation} Las colisiones totales entre moléculas de tipo 1 por unidad de tiempo y de volumen, vendrán dadas por: \begin{equation} Z_{11}=\frac{1}{\sqrt{2}\pi d_1^2}\left(\frac{8kT}{\pi m}\right)^{1/2}\left(\frac{N_1}{V}\right) \end{equation} Obsérvese que es necesario dividir la ecuación entre 2 para no contar dos veces la misma colisión.</v_{11}>



