The kinetic theory allows us to calculate the frequency of collisions between molecules. We assume that the molecules are rigid spheres of diameter d and we neglect intermolecular forces except at the moment of collision. At high pressures, intermolecular forces cannot be neglected and the equations obtained are not applicable. We will use the following notation:
- $z_{12}$: number of collisions per unit time (frequency of collisions) that a molecule of gas 1 experiences with the molecules of gas 2.
- $z_{11}$: frequency of collisions that a molecule of gas 1 experiences with other molecules of gas 1.
- $Z_{12}$: total frequency of collisions between molecules of gas 1 with those of gas 2 per unit volume.
Let $N_1$ be molecules of gas 1 with diameter $d_1$ and $N_2$ be molecules of gas 2 with diameter $d_2$. Molecules move at average speeds $\bar{v}_1$ and $\bar{v}_2$.
We begin by calculating the collisions of type 1 with type 2 molecules $(z_{12})$. Let us consider the type 2 molecules at rest and the type 1 ones moving at velocity $\bar{v}_{12}$, the relative average speed of the type 1 molecules with respect to the type 2 ones.
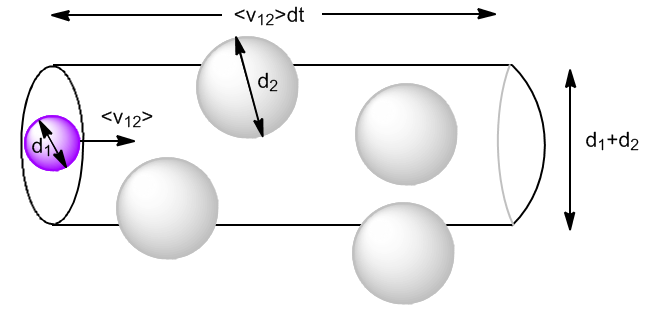
In one dt, the molecule 1 will travel a distance $\bar{v}_{12}dt$ and will collide with all the molecules 2 that are inside a cylinder of diameter $d_1+d_2$. The volume of the cylinder is:
\begin{equation} V_{cil}\frac{N_2}{V}=\pi\left(\frac{d_1+d_2}{2}\right)^2\bar{v}_ {12}dt\frac{N_2}{V}=\pi d_{12}^{2}\bar{v}_{12}dt\frac{N_2}{V} \end{equation}
Where $d_{ 12}$ the collision diameter. We can also define a cross section, $\sigma_{12}=\pi d_{12}^2$.
The collisions that a type 1 particle undergoes with those of type 2 per unit time, called the collision frequency $z_{12}$, we are left with: \begin{equation} z_{12}=\sigma_{12}\bar{ v}_{12}\frac{N_2}{N} \end{equation}
We only need to obtain the magnitude of the average relative velocity, $v_{12}>$. considering collisions at 90º (mean between 0º and 180º) $\bar{v}_{12}^2=\bar{v}_1^2+\bar{v}_2^2$. Since $\bar{v}=\sqrt{\frac{8RT}{\pi M}}$
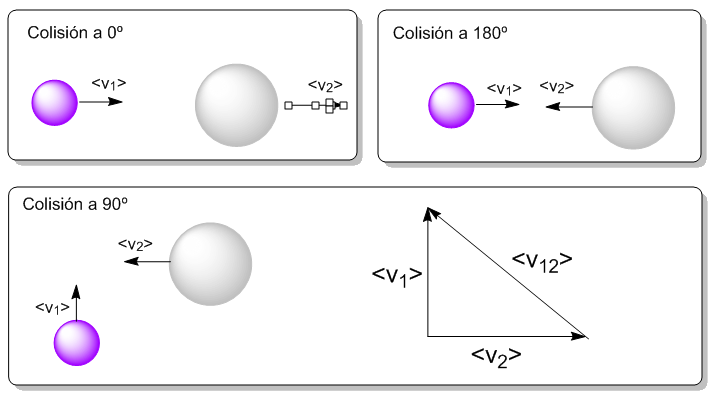
\begin{equation} \bar{v}_{12}^2=\frac{8RT}{\pi M_1}+\frac{8RT}{\pi M_2} \end{equation}
Substituting into $z_{12}$
\begin{equation} z_{12}=\sigma_{12}\left[\frac{8RT}{\pi}\left(\frac{1}{M_1}+\frac{1}{M_2}\right )\right]^{1/2}\frac{N_2}{V} \end{equation}
We define the total frequency of collisions of type 1 molecules with type 2 molecules as: $Z_{12}=z_{12} \cdot N_1$. Since it is a very large number, it is usually taken per unit volume:
\begin{equation} Z_{12}=z_{12}\frac{N_1}{V} \end{equation}
Substituting $z_{12}$
\begin{equation} Z_{12}=\sigma_{12}\left[\frac{8RT}{\pi}\left(\frac{1}{M_1}+\frac{1}{M_2}\right)\right]^{1/2}\frac{N_1}{V}\frac{N_1}{V} \end{equation}
In general $z_{12}\neq z_{21}$ but $Z_{12}= Z_{21}$
Collisions between type 1 molecules are:
\begin{equation} z_{11}=\pi d_{11}^2<v_{11}>\frac{N_1}{V} \end{equation}
where
\begin{equation} d_{11}=\frac{d_1+d_1}{2}=d_1 \end{equation}
\begin{equation} \bar{v}_{11}^2 =\bar{v}_1^2+ \bar{v}_1^2=2\bar{v}_1^2=2\frac{8kT}{\pi m} \end{equation}
Substituting
\begin{equation} z_{11}=\sqrt{2 }\pi d_1^2\left(\frac{8kT}{\pi m}\right)^{1/2}\frac{N_1}{V} \end{equation}
The total collisions between type 1 molecules by unit of time and volume, will be given by:
\begin{equation} Z_{11}=\frac{1}{\sqrt{2}\pi d_1^2}\left(\frac{8kT}{\pi m }\right)^{1/2}\left(\frac{N_1}{V}\right) \end{equation}
Note that it is necessary to divide the equation by 2 so as not to count the same collision twice $<v_ {11}>$



