Cuando el hamiltoniano es independiente del tiempo, la función de estado puede escribirse como un producto de una función del tiempo por una función de la posición.![]()
Sustituyendo en la ecuación de Schrödinger dependiente del tiempo: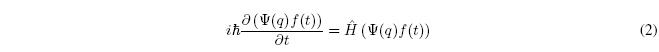
Como \(\Psi\) no depende de t y \(\hat{H}\) tampoco, podemos sacar \(\Psi (q)\) de la derivada temporal y \(f(t)\) del hamiltoniano.![]()
Dividiendo los terminos de la ecuación (3) por \(f(t)\Psi (q)\) nos da:
El miembro de la izquierda depende sólo de t y el de la derecha sólo de las coordenadas q. Así, la igualdad sólo es posible si ambos términos son iguales a una constante que llamaremos E.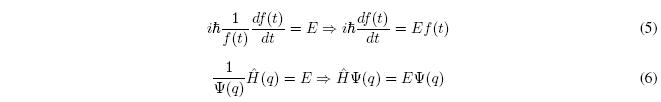
La primera ecuación nos da la evolución temporal del sistema (ecuación de Schrödinger temporal). La segunda ecuación es la ecuación de Schödinger espacial o independiente del tiempo.
Integramos la ecuación de Schrödinger temporal:
Donde C es la constante de integración. Tomando antilogaritmos se obtiene la función f(t).![]()
La constante A puede ser incluida en la función \(\Psi (q)\) como un factor multiplicativo, así, podemos escribir la ecuación anterior como:![]()
Por tanto, en aquellos sistemas en los que el hamiltoniano no depende de t, la función de estado puede escribirse:![]()
Los estados de un sistema físico que pueden escribirse de la forma anterior se caracterizan por tener una energía constante y se denominan estados estacionarios. Los estados estacionarios se caracterizan por tener una densidad de probabilidad independiente del tiempo.![]()
Por tanto, para un sistema con \(\hat{H}\) independiente de t, la energía total es constante y la probabilidad de que la partícula tenga sus coordenadas entre \(q\) y \(q+dq\) no cambia con el tiempo.



