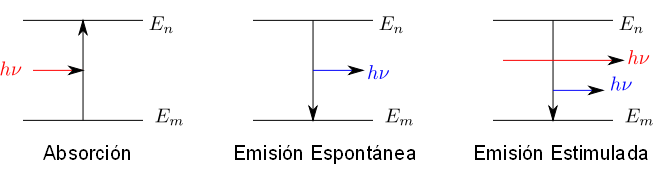
Los espectros de absorción se producen cuando la materia absorbe un fotón de frecuencia $\nu$ cuya energía es $h\nu$ y pasa de un estado de energía inferior $E_m$ a otro de energía superior $E_n$. Debe cumplirse que la diferencia de energía entre estos estados sea igual a la energía del fotón absorbido, $E_n - E_m = h\nu$.
En los espectros de emisión espontánea una molécula pasa de un estado de energía $E_n$ a otro inferior $E_m$, emitiendo un fotón de energía $E_n - E_m =h\nu$
La emisión de radiación por parte de la materia se puede favorecer por exposición a la radiación electromagnética. En este caso se habla de emisión estimulada. Exponiendo la molécula a radiación electromagnética de frecuencia $E_n - E_m =h\nu$ aumenta la probabilidad de que ocurra la transición desde el estando n al m.
De lo comentado anteriormente se deduce que la radiación electromagnética debe tener una frecuencia adecuada para producir una transición entre estados. Los estados electrónicos de una molécula están más espaciados que los vibracionales, y estos a su vez más espaciados que los rotacionales. Las transiciones electrónicas se producen por absorción en la región ultravioleta-visible (UV) (radiación energética). Las transiciones vibracionales producen absorción en la región infrarroja (IR). Por último, las transiciones rotacionales se producen por absorción en la región del microondas.
¿Verdadero o Falso?
(a) Cuando una molécula absorbe fotones se produce una transición a un estado estacionario de energía $E_k$, la frecuencia de absorción $\nu$ satisface $E_k=h\nu$.
(b) Cuando una molécula emite un fotón de frecuencia $\nu$, experimenta un cambio de energía que viene dado por $\Delta E=h\nu$.
(c) Cuando una molécula absorbe un fotón de frecuencia $\nu$, experimenta un cambio de energía dado por $\Delta E=h\nu$.
(d) La longitud de onda mayor de una transición corresponde con la menor diferencia de energía entre los dos niveles involucrados en la transición.
(e) Exponiendo una molécula en el estado n a una radiación electromagnética de frecuencia $\nu=(E_n -E_m)/h\nu$ se incrementará la probabilidad de que la molécula tenga una transición hasta el estado de menor energía m con la emisión de un fotón de frecuencia $\nu$.}



