La deducción es análoga a la conductividad térmica o viscosidad con al diferencia de que se transporta materia.
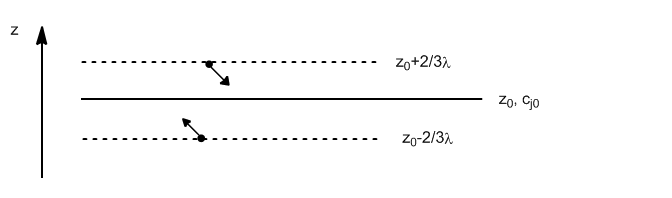
El flujo neto de materia (en moles) que atraviesa el plano $z_0$ viene dado por: \begin{equation} J_z=J_{\uparrow}-J_{\downarrow}=\frac{dN_{\uparrow}}{N_A}-\frac{dN_{\downarrow}}{N_A} \end{equation} El número de moléculas que atraviesan $z_0$ desde abajo viene dado por: \begin{equation} dN_{\uparrow}=\frac{1}{4}\bar{v}\frac{N_{\uparrow}}{V}\frac{N_A}{N_A}=\frac{1}{4}\bar{v}N_A\frac{c_{\uparrow}}{V} \end{equation} Sustituyendo $c_{\uparrow}$ por la concentración de moléculas en el plano $z_0-2/3\lambda$ \begin{equation} dN_{\uparrow}=\frac{1}{4}\bar{v}N_A\left[c_{j0}-\frac{2}{3}\lambda\left(\frac{dc_j}{dz}\right)_0\right] \end{equation}
De forma análoga escribimos el número de moléculas que cruzan $z_0$ desde arriba. \begin{equation} dN_{\downarrow}=\frac{1}{4}\bar{v}N_A\left[c_{j0}+\frac{2}{3}\lambda\left(\frac{dc_j}{dz}\right)_0\right] \end{equation} Sustituyendo en $J_z$ \begin{equation} J_z=\frac{1}{4}\bar{v}\frac{-4}{3}\lambda\frac{dc_j}{dz}\frac{-1}{3}\bar{v}\lambda\frac{dc_j}{dz} \end{equation} De donde se deduce que el coeficiente de difusión viene dado por: \begin{equation} D=\frac{1}{3}\bar{v}\lambda \end{equation} Un tratamiento riguroso nos da: \begin{equation} D=\frac{3\pi}{16}\lambda \bar{v} \end{equation} Reemplazando $\lambda=\frac{1}{\sqrt{2}\pi d^2}\frac{kT}{P}$ y $\bar{v}=\left(\frac{8kT}{\pi m}\right)^{1/2}$, nos queda: \begin{equation} D=\frac{8}{8d^2}\left(\frac{kT}{\pi m}\right)^{1/2}\frac{kT}{P} \end{equation}



