Permite determinar el flujo laminar estacionario (dV/dt) para un fluido incompresible, de viscosidad constante, a través de un tubo cilíndrico de radio r.
Consideremos un fluido que circula por una conducción cilíndrica de radio r. Tomemos un elemento infinitesimal de longitud z y radio interno s, con una presión $p_1$ a la entrada y $p_2$ a la salida.
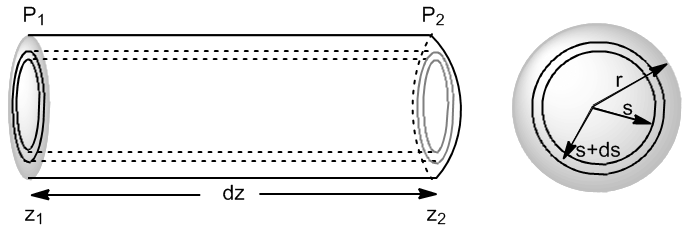
Vamos a escribir las fuerzas que actúan sobre la capa de fluido situada entre s y s+ds.
- Fuerzas hidrostáticas de presión $(F=PS)$
- Fuerza debida a la presión de entrada: $F_1=2\pi SdS\cdot P_1$
- Fuerza debida a la presión de salida: $F_2=-2\pi SdS\cdot P_2$
- Fuerzas de rozamiento.
- Rozamiento con la parte interior $F_{RI}=-\eta\cdot 2\pi Sdz(dV/dS)_s$. Como el gradiente de velocidad es negativo la fuerza de rozamiento es positiva ya que las capas internas van más rápidas y aceleran la capa de fluido considerada.
- Rozamiento con la pared exterior $F_{RE}=\eta\cdot 2\pi (S+dS)dz(dV/dS)_{S+dS}$. Esta fuerza de rozamiento es negativa ya que se opone al movimiento de la capa considerada.
Una vez alcanzado el régimen estacionario: $\sum\vec{F_i}=0$
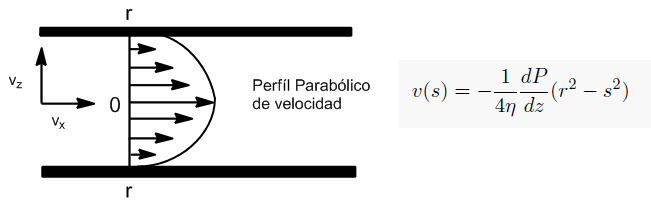
\begin{equation} 2\pi SdS\cdot P_1-2\pi SdS\cdot P_2-\eta2\pi Sdz(dv/dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{S+dS}=0 \end{equation} Dado que $P_2=P_1+dP$ \begin{equation} 2\pi SdS\cdot P_1-2\pi SdS(P_1+dP)-\eta2\pi Sdz(dv/dS)_S+\eta 2\pi (S+dS)dz(dV/dS)_{S+dS}=0 \end{equation} Simplificando las expresión anterior \begin{equation} -\cancel{2\pi} SdSdP+ \cancel{2\pi}\eta dz\left[(S+dS)(dv/dS)_{S+dS}-S(dv/dS)_s\right]=0 \end{equation} Teniendo en cuenta la definición de derivada: $df(x)=f(x+dx)-f(x)$, podemos escribir la expresión anterior de la siguiente forma \begin{equation} -SdSdP+\eta dzd\left[s\frac{dv}{dS}\right]=0 \end{equation} \begin{equation} \frac{dP}{dz}SdS=\eta d\left[s\frac{dv}{dS}\right] \end{equation} Integrando con el gradiente de presión constante \begin{equation} \frac{dP}{dz}\frac{S^2}{2}=\eta S\frac{dv}{dS} + C \end{equation} Dado que dv/ds no puede ser infinito, si haciendo S=0 \begin{equation} 0=0+C \; \rightarrow \;C=0 \end{equation} Despejando dv \begin{equation} dv=\frac{1}{2\eta}\frac{dP}{dz}SdS \end{equation} Integrando de nuevo \begin{equation} v(S)=\frac{1}{2\eta}\frac{dP}{dz}\frac{s^2}{2}+C \end{equation} Calculamos la nueva constante de integración, C, sabiendo que en las paredes de la conducción el flujo se anula, $v(S=r)=0$ \begin{equation} 0=\frac{1}{2\eta}\frac{dP}{dz}\frac{r^2}{2}+C \;\rightarrow C=-\frac{1}{4\eta}\frac{dP}{dz}r^2 \end{equation} Reemplazando la constante de integración en la ecuación de la velocidad v(s) \begin{equation} v(s)=-\frac{1}{4\eta}\frac{dP}{dz}(r^2-s^2) \end{equation} Ecuación que nos da un perfil parabólico para la velocidad de un fluido en estado estacionario.
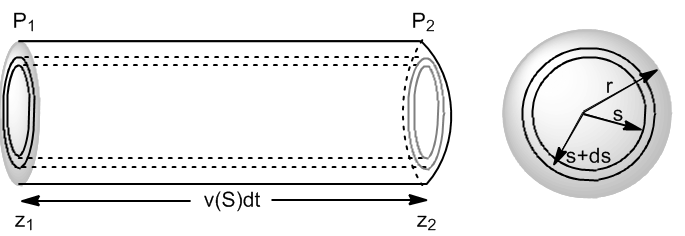
En un dt el volumen de fluido que se ha desplazado por la corona de espesor ds es: $dV=2\pi SdS\cdot v(s)dt$. El volumen total que circula por la conducción lo obtenemos integrando desde S=0 hasta S=r.
\begin{equation} \frac{dV}{dt}=\int_{0}^{r}2\pi S\cdot v(S)dS \end{equation} Sustituyendo v(S) por su valor: \begin{equation} \frac{dV}{dt}=2\pi \int_{0}^{r}S\frac{-1}{4\eta}(r^2-s^2)\frac{dP}{dz}=\frac{-\pi}{2\eta}\frac{dP}{dz}\left[\frac{r^4}{2}-\frac{r^4}{4}\right] \end{equation} Haciendo la diferencia y simplificando se obtiene la ecuación diferencial de Poiseuille. \begin{equation} \frac{dV}{dt}=\frac{-\pi r^4}{8\eta}\frac{dP}{dz} \end{equation} En el caso de los líquidos podemos integrar ya que son poco compresibles y el volumen es independiente de la presión. \begin{equation} \frac{\Delta V}{\Delta t}=\frac{-\pi r^4}{8\eta}\frac{\Delta P}{\Delta z} \end{equation}



