Los fotones de infrarrojo producen transiciones vibracionales, aunque no electrónicas, dando lugar a espectros de rotación-vibración. Para que se observe el espectro de rotación vibración es necesario que cambie el momento dipolar durante la vibración. Por ello, las moléculas diatómicas homonucleares no presentan espectro IR de rotación vibración.
El espectro de rotación-vibración se observa generalmente como un espectro de absorción con transiciones $\Delta v =+1 (+2, +3, ...)$ donde las transiciones entre paréntesis, llamadas sobretonos, son menos probables. Simultáneamente $\Delta J =+1$ produciéndose transiciones entre niveles rotacionales simultáneas a las vibracionales.
El espectro de rotación-vibración consta de una serie de bandas que corresponden a transiciones entre dos niveles vibracionales $v''$ y $v'$ y de una serie de líneas, correspondientes a transiciones rotacionales.
Bandas vibracionales
En principio, calcularemos la frecuencia de una transición donde v cambia pero J es cero tanto en el estado inicial como en el final. Esta transición nos da la posición de la banda: origen.
\begin{equation}\label{11} \bar{\nu}_{o}=\frac{E_{v'}-E_{v''}}{hc} \end{equation}
La energía vibracional para el estado v viene dada por:
\begin{equation}\label{12} E_{v}=h\nu_{e}\left(v+\frac{1}{2}\right)-h\nu_{e}x_{e}\left(v+\frac{1}{2}\right)^2 \end{equation}
La banda fundamental se obtiene sustituyendo la ecuación (\ref{12}) en (\ref{11})
\begin{equation}\label{13} \bar{\nu}_o =\bar{\nu}_e\left(v'+\frac{1}{2}\right)-\bar{\nu}_e x_e\left(v'+\frac{1}{2}\right)^2-\bar{\nu}_e\left(v'+\frac{1}{2}\right)+\bar{\nu}_ex_e\left(v'+\frac{1}{2}\right)^2 \end{equation}
Desarrollando los cuadrados y sacando factor común a $\bar{\nu}_ex_e$
\begin{equation}\label{14} \bar{\nu}_o=\bar{\nu}_e(v'-v'')-\bar{\nu}_ex_e\left[v'^{2}+\frac{1}{4}+v'-v''^{2}-\frac{1}{4}-v''\right] \end{equation}
Por tanto, la banda obtenida por transiciones entre niveles vibracionales sin cambio en el número cuántico rotacional nos queda:
\begin{equation}\label{15} \bar{\nu}_o=\bar{\nu}_e(v'-v'')-\bar{\nu}_{e}x_{e}[v'(v'+1)-v''(v''+1)] \end{equation}
Dado que el nivel vibracional fundamental es el más poblado, la transición ($0\rightarrow 1$) da la banda más intensa, llamada banda fundamental. Calculamos su frecuencia haciendo $v''=0$ y $v'=1$ en (\ref{15})
\begin{equation}\label{16} \bar{\nu}_o=\bar{\nu}_e-2\bar{\nu}_ex_e \end{equation}
La transición ($0\rightarrow 2$)es el primer sobretono, obtenemos su frecuencia haciendo $v''=0$ y $v'=2$ en la ecuación (\ref{15})
\begin{equation}\label{17} \bar{\nu}_o=2\bar{\nu}_e-6\bar{\nu}_ex_e \end{equation}
Dado que el término debido a la anarmonicidad $\bar{\nu}_ex_e$ es mucho más pequeño que $\bar{\nu}_e$ la banda fundamental y los sobretonos son aproximadamente $\bar{\nu}_e,2\bar{\nu}_e,3\bar{\nu}_e......$
Las bandas con $v'' >0$ son muy débiles y se llaman bandas calientes.
Estructura rotacional de cada banda
La regla de selección para las transciones rotacionales es $\Delta J=\pm 1$. Las transiciones con $\Delta J=+1$ dan lugar a la rama R del espectro, mientras que las transiciones con $\Delta J=-1$ generan la rama P.
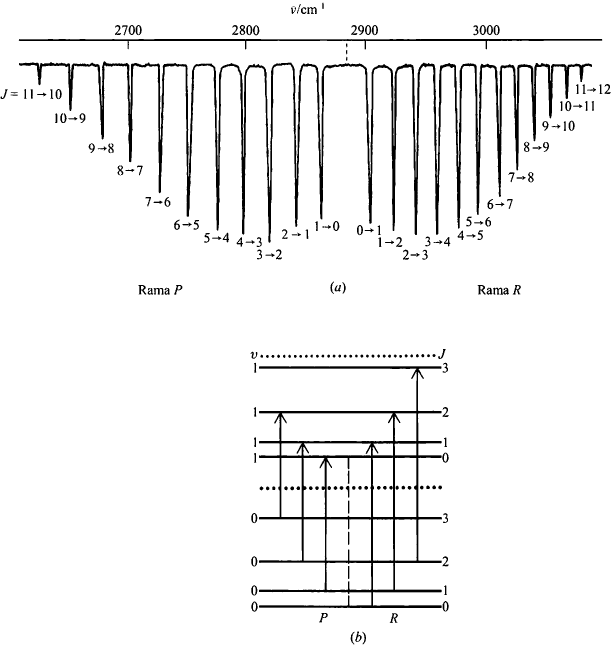
La energía rotacional viene dada por la ecuación:
\begin{equation}\label{18} E_J=hB_eJ(J+1) \end{equation}
Para una transición desde $J''$, el nivel rotacional inferior, a $J'$ el nivel rotacional superior, con un cambio en los niveles vibracionales de $v''$ a $v'$ se produce absorción de radiación a la siguiente frecuencia:
\begin{equation}\label{19} \bar{\nu}=\bar{\nu_e}(v'-v'')-\bar{\nu}_ex_e[v'(v'+1)-v''(v''+1)]+\bar{B}_eJ'(J'+1)-\bar{B}_eJ''(J''+1) \end{equation}
Comparando la ecuación (\ref{15}) con la (\ref{19}) observamos que los dos primeros sumandos corresponden con la banda origen.
\begin{equation}\label{20} \bar{\nu}=\bar{\nu}_{o}+\bar{B}_eJ'(J'+1)-\bar{B}_eJ''(J''+1) \end{equation}
El espectro roto-vibracional está formado por dos ramas, llamadas R y P. Las líneas de la rama R proceden de transiciones $J'=J''+1$.
\begin{equation}\label{21} \bar{\nu}_R=\bar{\nu}_o+\bar{B}_e(J''+1)(J''+2)-\bar{B}_eJ''(J''+1)=\bar{\nu}_o+2\bar{B}_e(J''+1) \end{equation}
Las líneas que componen la rama P se obtienen por transiciones $J'=J''+1$
\begin{equation}\label{22} \bar{\nu}_P=\bar{\nu}_o+\bar{B}_e(J''+1)J''-\bar{B}_eJ''(J''+1)=\bar{\nu}_o-2\bar{B}_eJ'' \end{equation}
$J''=0"$ se excluye en las líneas de la rama P ya que no puede ser -1.



