Infrared photons produce vibrational, though not electronic, transitions, giving rise to rotation-vibration spectra. For the spectrum of rotational vibration to be observed, it is necessary for the dipole moment to change during vibration. For this reason, homonuclear diatomic molecules do not present IR spectrum of rotational vibration.
The rotation-vibration spectrum is generally observed as an absorption spectrum with transitions $\Delta v =+1 (+2, +3, ...)$ where the transitions in parentheses, called overtones, are less likely. Simultaneously $\Delta J =+1$ producing transitions between rotational levels simultaneous to the vibrational ones.
The rotation-vibration spectrum consists of a series of bands that correspond to transitions between two vibrational levels $v''$ and $v'$ and a series of lines, corresponding to rotational transitions.
Vibration bands
In principle, we will calculate the frequency of a transition where v changes but J is zero in both the initial and final states. This transition gives us the position of the band: origin.
\begin{equation}\label{11} \bar{\nu}_{o}=\frac{E_{v'}-E_{v''}}{hc} \end{equation}
The vibrational energy for state v is given by:
\begin{equation}\label{12} E_{v}=h\nu_{e}\left(v+\frac{1}{2}\right)-h\nu_{e}x_{e}\left( v+\frac{1}{2}\right)^2 \end{equation}
The fundamental band is obtained by substituting the equation (\ref{12}) in (\ref{11})
\begin{equation}\label{13} \bar{\nu}_o =\bar{\nu}_e\left(v'+\frac{1}{2}\right)-\bar{\nu}_e x_e\left(v'+\frac{1}{2}\right)^2-\bar{\nu}_e\left(v'+\frac{1}{2}\right)+\bar{\ nu}_ex_e\left(v'+\frac{1}{2}\right)^2 \end{equation}
Expanding the squares and taking a common factor of $\bar{\nu}_ex_e$
\begin{equation}\label{14} \bar{\nu}_o=\bar{\nu}_e(v'-v'')-\bar{\nu}_ex_e\left[v'^{2} +\frac{1}{4}+v'-v''^{2}-\frac{1}{4}-v''\right] \end{equation}
Therefore, the band obtained by transitions between vibrational levels without change in the rotational quantum number remains:
\begin{equation}\label{15} \bar{\nu}_o=\bar{\nu}_e(v'-v'')-\bar{\nu}_{e}x_{e}[v '(v'+1)-v''(v''+1)] \end{equation}
Since the fundamental vibrational level is the most populous, the transition ($0\rightarrow 1$) gives the most intense band, called the fundamental band. We calculate its frequency by setting $v''=0$ and $v'=1$ in (\ref{15})
\begin{equation}\label{16} \bar{\nu}_o=\bar{\nu}_e-2\bar{\nu}_ex_e \end{equation}
The transition ($0\rightarrow 2$) is the first overtone, we obtain its frequency by setting $v''=0$ and $v'=2$ in the equation (\ref{15})
\begin{equation}\label{17} \bar{\nu}_o=2\bar{\nu}_e-6\bar{\nu}_ex_e \end{equation}
Since the term due to anharmonicity $\bar{\nu}_ex_e$ is much smaller than $\bar{\nu}_e$ the fundamental band and overtones are approximately $\bar{\nu}_e,2\ bar{\nu}_e,3\bar{\nu}_e......$
Bands with $v''>0$ are very weak and are called hot bands.
Rotational structure of each band
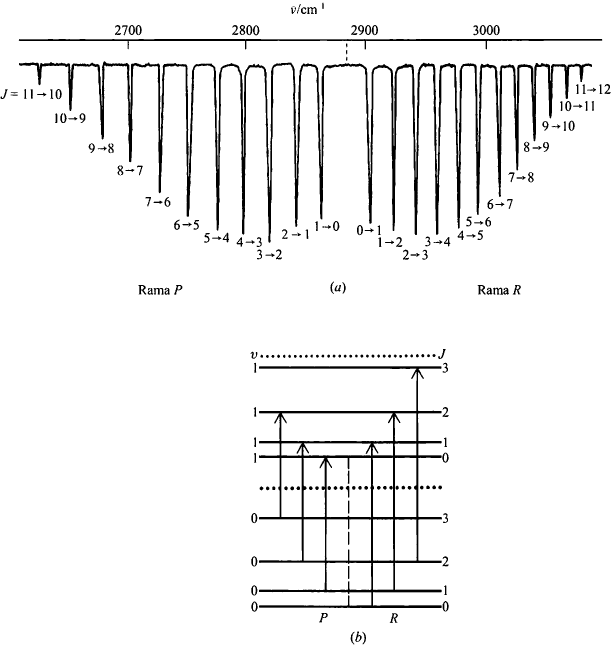
The selection rule for rotational transitions is $\Delta J=\pm 1$. Transitions with $\Delta J=+1$ give rise to the R branch of the spectrum, while transitions with $\Delta J=-1$ give rise to the P branch.
The rotational energy is given by the equation:
\begin{equation}\label{18} E_J=hB_eJ(J+1) \end{equation}
For a transition from $J''$, the lower rotational level, to $J'$, the upper rotational level, with a change in vibrational levels from $v''$ to $v'$ radiation absorption occurs at the following frequency:
\begin{equation}\label{19} \bar{\nu}=\bar{\nu_e}(v'-v'')-\bar{\nu}_ex_e[v'(v'+1)-v ''(v''+1)]+\bar{B}_eJ'(J'+1)-\bar{B}_eJ''(J''+1) \end{equation}
Comparing equation (\ref{15}) with (\ref{19}) we observe that the first two addends correspond to the original band.
\begin{equation}\label{20} \bar{\nu}=\bar{\nu}_{o}+\bar{B}_eJ'(J'+1)-\bar{B}_eJ'' (J''+1) \end{equation}
The rotational-vibrational spectrum is formed by two branches, called R and P. The lines of the R branch come from $J'=J''+1$ transitions.
\begin{equation}\label{21} \bar{\nu}_R=\bar{\nu}_o+\bar{B}_e(J''+1)(J''+2)-\bar{B }_eJ''(J''+1)=\bar{\nu}_o+2\bar{B}_e(J''+1) \end{equation}
The lines that make up the branch P are obtained by transitions $J'=J''+1$
\begin{equation}\label{22} \bar{\nu}_P=\bar{\nu}_o+\bar{B}_e(J''+1)J''-\bar{B}_eJ'' (J''+1)=\bar{\nu}_o-2\bar{B}_eJ'' \end{equation}
$J''=0"$ is excluded on the P branch lines since it cannot be -1.



