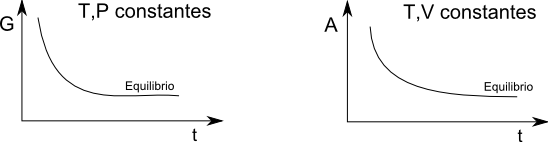
Empleando la ecuación (\ref{7}) obtendremos el criterio de equilibrio a T y V constantes. Debemos tener en cuenta que estas condiciones suponen $dV=0$ y $dT=0$. Sustituyendo en (\ref{7}) $dw=-PdV$ además de sumar y restar $SdT$ se obtiene. \begin{equation} dU\leq TdS +SdT-sdT -PdV \end{equation} Como $d(TS)=TdS+SdT$ la ecuación anterior nos queda: \begin{equation} dU\leq d(TS)-SdT-PdV \end{equation} Pasando el término $d(TS)$ al primer término de la desigualdad \begin{equation} d(U-TS)\leq -SdT-PdV \end{equation} Manteniendo T y V constantes durante el proceso, $dT=dV=0$ \begin{equation} d(U-TS)\leq 0 \end{equation}
Esto significa que durante un proceso irreversible (reacción química o transferencia de materia entre fases) la función de estado $U-TS$ disminuye hasta el equilibrio. Una vez alcanzado el equilibrio esta función se mantiene constante.\\ Por tanto, el criterio de equilibrio a T, V constantes consiste en minimizar la función de estado $U-TS$. Esta función se denomina energía libre de Helmholtz, y se representa por A. \begin{equation} A=U-TS \end{equation} Por último nos queda encontrar el criterio de equilibrio material a T, P constantes. Sumando y restando a la ecuación (\ref{7}) $SdT$ y VdP: \begin{equation} dU \leq TdS+SdT-SdT-PdV+VdP-VdP \end{equation} Agrupando: \begin{equation} dU\leq d(TS)-SdT-d(PV)+VdP \end{equation} \begin{equation} d(U+PV-TS)\leq-SdT-VdP \end{equation} Teniendo en cuenta que $dT=dV=0$ y que $H=U+PV$ \begin{equation} d(H-TS)\leq 0 \end{equation} La función de estado $H-TS$ se llama energía libre de Gibbs y se representa por G. \begin{equation} G=H-TS \end{equation} La función G disminuye durante la aproximación del sistema termodinámico al equilibrio material, alcanzando su valor mínimo en el equilibrio.