Partiendo del potencial químico de un soluto según el convenio II \begin{equation} \mu_{i}=\mu_{II,i}^{0}+RTln\gamma_{II,i}x_i \end{equation} La molalidad del componente i viene dada por, $m_i=\frac{n_i}{n_AM_A}$ donde $M_A$ es el peso molecular del disolvente. Dado que el disolvente es muy abundante podemos aproximar los moles de A por los totales y suponer que, $x_i=\frac{n_i}{n_A}$.
Sustituyendo esta fracción molar en la ecuación del potencial químico \begin{equation} \mu_i=\mu_{II,i}^{0}+RTln\left(\gamma_{II,i}m_ix_AM_A\frac{m^{0}}{m^{0}}\right) \end{equation}
En esta última ecuación multiplicamos y dividimos por $m^0$ con el objetivo de separar el neperiano en dos sumandos adimiensionales. \begin{equation} \mu_i=\underbrace{\mu_{II,i}^{0}+RTln(M_Am^0)}_{\mu_{m,i}^{0}}+RTln(\underbrace{x_A\gamma_{II,i}}_{\gamma_{m,i}}m_i/m^0) \end{equation} Por tanto, \begin{equation} \mu_{i}=\mu_{m,i}^{0}+RTln\gamma_{m,i}\frac{m_i}{m^0} \end{equation} Donde $\gamma_{m,i}\rightarrow 1$ cuando $x_A\rightarrow 1$ , $\gamma_{m,i}$ es el coeficiente de actividad en la escala de molalidades.
El potencial químico normal en la escala de molalidades $\mu_{m,i}^{0}$ se define como un estado ficticio en el cual la molalidad del soluto en la disolución es $m_i=1\;mol/kg$ y la disolución se comporta como diluida ideal $\gamma_{m,i}\rightarrow 1$
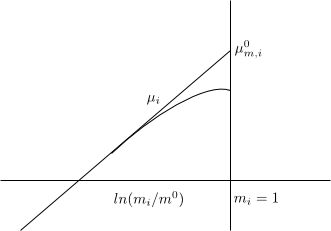
Con $m_i$ pequeños $\gamma_{m,i}\rightarrow 1$, comportamiento ideal y la gráfica es un línea recta.
En la escala de concentraciones molares el potencial químico se escribe: \begin{equation} \mu_i=\mu_{c,i}^{0}+RTln\left(\gamma_{c,i}\frac{c_i}{c^0}\right) \end{equation} Donde, $c^{0}=1\;mol/dm^3$, ademas $a_{c,i}=\gamma_{c,i}\frac{c_{i}}{c^0}$.



