We are going to calculate the collision frequency of gas molecules with the wall of a container in a dt.
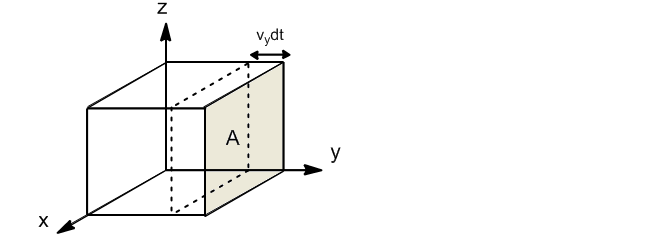
If we take the wall perpendicular to the y-axis, only molecules with velocity component y will collide against the wall. The fraction of molecules with component y of velocity between $v_y$ and $v_y+dv_y$ is given by:
\begin{equation} \frac{dN_{v_y}}{N}=g(v_y)dv_y \end{equation}
Only the molecules that are at a distance $v_ydt$ from the wall will be able to collide against it in the dt. The volume of the box in which the molecules that can hit the wall are found will be: $V'=Av_ydt$. Dividing this volume by the total $V'/V$, the fraction of molecules that due to their proximity to the wall can collide is obtained.
Multiplying the number of molecules that have a velocity between $v_y$ and $v_y+dv_y$ by the fraction of molecules that can reach the wall in dt we obtain:
\begin{equation} dN_{p,v_y}=\frac {V'}{V}dN_{v_y}=\frac{Av_ydt}{V}Ng(v_y)dv_y \end{equation}
Integrating over the interval $v_y[0,\infty]$, we obtain the total collisions:
\begin{equation} dN_p=\int_{0}^{\infty}\frac{Av_ydt}{V}Ng(v_y)dv_y=\frac{ANdt}{V}\int_{0}^{\infty}v_yg( v_y)dv_y \end{equation}
Evaluating the average of $v_y$
\begin{equation} \int_{0}^{\infty}g(v_y)v_ydv_y=\int_{0}^{\infty}\left(\ frac{m}{2\pi kT}\right)^{1/2}e^{\frac{-mv_{y}^{2}}{2kT}}v_ydv_y=\left(\frac{kT}{ 2\pi m}\right)^{1/2} \end{equation}
Taking this result to the equation of collisions per unit of time.
\begin{equation} dN_p=A\frac{NAdt}{V}\left(\frac{kT}{2\pi m}\right)^{1/2} \end{equation}
This last equation represents the number of molecules that collide against the wall of area A in a dt.
We define the collision frequency per unit area and time as:$Z_p=\frac{1}{A}\frac{dN_p}{dt}$
\begin{equation} Z_p=\frac{N}{V}\left (\frac{kT}{2\pi m}\right)^{1/2}=\frac{1}{4}\left(\frac{8kT}{2\pi m}\right)^{1 /2}\frac{N}{V}=\frac{1}{4}\bar{v}\frac{N}{V} \end{equation}
Where $\bar{v}$ is the magnitude of the average speed.
\begin{equation} Z_p=\frac{1}{4}\bar{v}\frac{N}{V} \end{equation}
The frequency of collision depends on the density of the gas $(N/V)$ and the average velocity of the molecules. The higher the density and average speed, there will be a higher frequency of collisions. From the ideal gas equation of state, $PV=\frac{N}{N_A}RT$ and considering that $k=R/N_A$, we obtain $\frac{N}{V}=\frac{ P}{kT}$. With this result we can simplify the previous equation.
\begin{equation} Z_p=\frac{1}{4}\bar{v}\frac{N}{V}=\frac{1}{4}\left(\frac{8kT}{\pi m} \right)^{1/2}\frac{P}{kT} \end{equation}
Grouping terms we get:
\begin{equation} Z_p=\frac{P}{(2\pi mkT)^{1/ 2}} \end{equation}
Calculation of $Z_p$ for oxygen at 298K and 1atm gives: $2.7x10^{23}\;col/cm^2s$



