If a container containing a gas has a small hole of area $A_{or}$ and there is a vacuum outside the container, the molecules that collide with the hole escape from the container at a speed given by:
\begin{equation} \frac{dN}{dt}=\frac{-A_{or}P}{\left(2\pi mkT\right)^{1/2}} \end{equation}
The minus sign indicates that the molecules come out of the container. This phenomenon is called effusion, the effusion rates being inversely proportional to the square roots of the molecular masses.
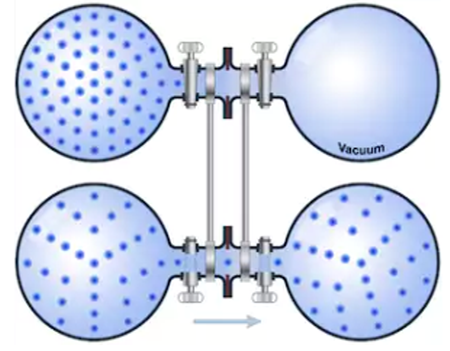
In order for Graham's Law to be fulfilled, it is necessary that the hole be very small, so that the gas escapes slowly and does not break the Maxwellian velocity distribution. The diameter of the hole must be substantially smaller than the distance the gas molecules travel between two collisions (mean free path), to avoid colliding with each other in the vicinity of the hole, which would give rise to a collective flow that breaks the Maxwell distribution



