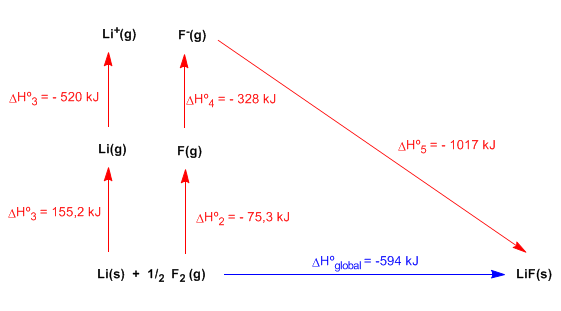
The lattice energy gives us a measure of the stability of an ionic compound, and is defined as the energy required to completely separate one mole of a solid ionic compound into its ions in the gaseous state. When the ions unite to form the crystal lattice heat is given off (exothermic process), the ionic compound is more stable than the separated ions. To break the ionic compound separating the ions that form it, it is necessary to give an energy (equal to that given off when formed) called reticular.
The Born-Haber cycle allows obtaining the lattice energy of an ionic compound through the following stages, analyzed for the formation of LiF(s): 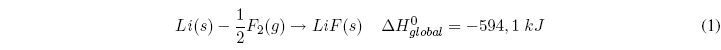
- Convert from solid lithium to gas. We apply the heat of sublimation of lithium: \(\Delta H_{sub}=155.2\;kJ/mol\)
![]()
- Dissociation of the fluorine molecule. Note that it is only necessary to dissociate half a mole: \(\Delta H_{dis}^{0}=150.6\;kJ/mol\)
![]()
- Ionization of 1 mole of lithium gas.
![]()
- Addition of 1 mole of electrons to fluorine gas.
![]()
- Combination of 1 mol of lithium and 1 mol of Fluorine to form the solid LiF compound.
![]()
The sum of the 5 stages gives us the global reaction and applying Hess' Law we can determine the lattice energy. 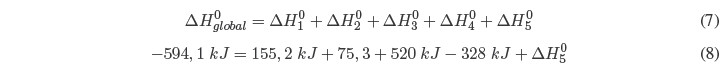
Solving for \(\Delta H^{0}_{5}\) ![]()