Conductivity measurements indicate that pure water is partially ionized. Ions are generated when some water molecules act as acids by donating protons to other water molecules that act as bases, according to the following equilibrium.
$H_2O + H_2O \rightleftharpoons H_3O^+ + OH^-$
This is a reversible reaction highly shifted to the left. The amounts of oxonium and hydroxide ions present in the medium are very small.
The equilibrium constant for this reaction is called the ionic product of water, $K_w$
$K_w=[H_3O^+][OH^-]=10^{-14}$
In pure water the concentrations of both ions are the same: $[H_3O^+]=[OH^-]=10^{-7}$
Since $K_w$ is a constant, at all times the product of the concentrations of oxonium and hydroxide ions must be $10^{-14}$. Therefore, if we add an acid to pure water, increasing the concentration of protons in the solution, the concentration of hydroxide ions must decrease to maintain the value of $K_w$
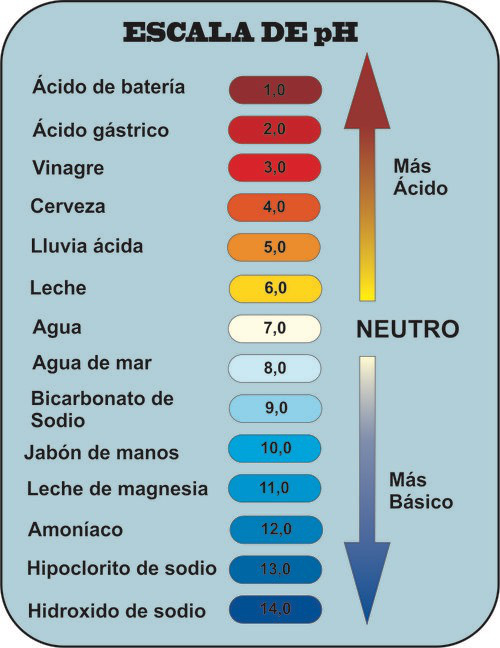 pH scale
pH scale
In 1909, the Danish chemist Soren Sorensen defined pH as:
$pH=-log[H_3O^+]$
The pH gives us the degree of acidity that a solution presents.
Thus, in pure water $[H_3O^+]=10^{-7}$ M and its $pH=-log(10^{-7})=7$.
- So we consider that all aqueous solutions at 25ºC with pH=7 are neutral.
- When the pH is greater than 7 the solution is basic.
- When the pH is less than 7 the solution is acidic.
We can also define the pOH:
$pOH=-log[OH^-]$
Given that $[H_3O^+][OH^-]=10^{-14}$, taking logarithms gives the relationship between pH and pOH:
$pH+pOH=14$



