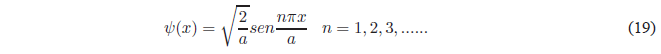Ahora vamos a introducir un sistema mecanocuántico sencillo, donde podemos aplicar los conceptos introducidos en la sección anterior. Este modelo se puede aplicar al movimiento traslacional monodimensional de las moléculas de un gas ideal, movimiento de electrones en metales e incluso al movimiento de electrones pi en hidrocarburos insaturados.
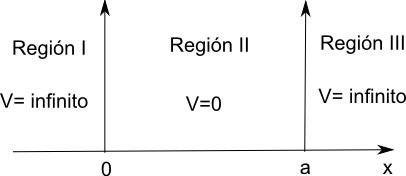
Consideremos una partícula de masa m que se mueve a lo largo del eje x sometida a un potencial nulo en la región situada entre las coordenadas 0 y a. Fuera de esta zona el potencial es infinito. La partícula no puede acceder a la zona de potencial infinito por lo que su movimiento queda limitado a la región 0,a.
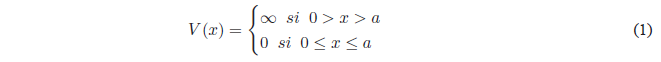
Planteamos la ecuación de Schrödinger:
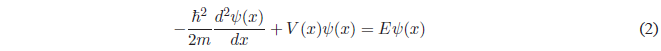
Resolución de la ecuación en las regiones I y III
En las regiones I y III \(V(x) = \infty\). La ecuación de Schrödinger tomará la siguiente forma:
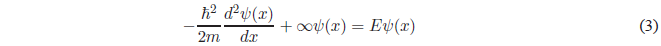
Esta ecuación también se puede expresar como:
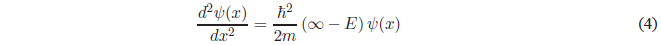
Despejando \(\psi(x)\)
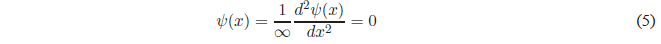
Por tanto, en las regiones I y III la función de onda es nula, lo cual implica una densidad de probabilidad nula y la particula no puede encontrarse en estas regiones de la caja. Una partícula no puede encontrarse en regiones donde la energia potencial sea infinita.
Resolución de la Ecuación de Schrödinger en la región II
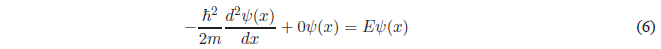
Despejando la derivada de mayor grado y pasando todo al primer miembro de la ecuación.
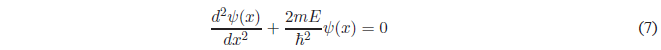
Por simplicidad llamaremos \(k=\frac{\sqrt{2mE}}{\hbar}\)
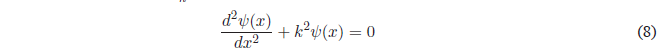
Se trata de una ecuación diferencial lineal, homogénea y de segundo orden cuya solución general es:
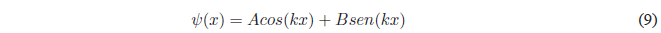
Las constantes A y B se determinan aplicando las condiciones límite que debe cumplir la función \(\psi(x)\) para que sea bien comportada.
Puesto que \(\psi(x)\) debe ser contínua, cumplirá las condiciones. \(\psi(x) \rightarrow 0\) si \(x \rightarrow 0\) y si \(x \rightarrow a\). Aplicando la primera condición:
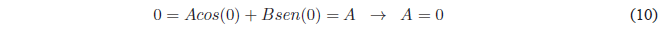
Dado que $A=0$ la ecuación nos queda: \(\psi(x)=Bsen(kx)\). Aplicando la condición límite en \(x=a\)
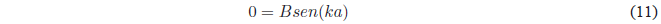
Una posible solución de esta última ecuación es \(B=0\), esta solución anula la función de onda e implicaría que la caja no tiene partícula (caja vacía). Por tanto, debe anularse el \(sen(ka)\)
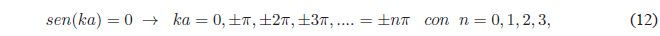
El valor \(n=0\) debe ser rechazado ya que anula la función de onda.
Elevando al cuadrado la ecuación anterior:
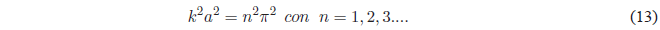
Teniendo en cuenta que \(k^2 =\frac{2mE}{\hbar^2}\) la ecuación anterior nos da:
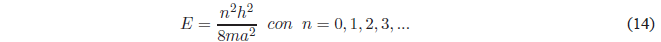
Como puede observarse en esta ecuación la energía sólo puede tomar ciertos valores (energía cuantizada) que vienen determinados por el número cuántico $n$. Solamente estos valores de energia permiten a la función \(\psi(x)\) satisfacer las condiciones de continuidad en \(x=0\) y \(x=a\).
Haciendo \(n=1\) obtenemos la energía del estado fundamental \(E_1 =\frac{h^2}{8ma^2}\). También puede observarse que la diferencia de energía entre dos niveles sucesivos decrece a medida que aumenta tanto n como la logitud de la caja.
Por último, obtendremos el valor de B normalizando la función de onda \(\psi(x)=Bsen\frac{n\pi x}{a}\). Normalizar consiste en igualar a 1 la probabilidad de encontrar la particula en todo el espacio.
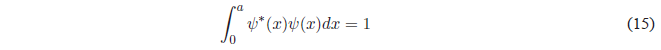
Sustituyendo \(\psi(x)\) por su valor:
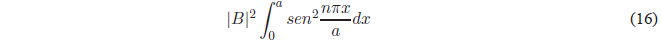
Utilizando la relación trigonométrica \(sen^2 x=\frac{1-cos2x}{2}\), se obtiene:
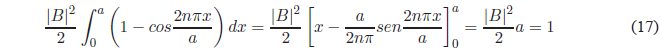
Despejando B
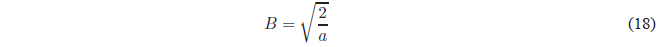
Sustituyendo B en la función de onda
