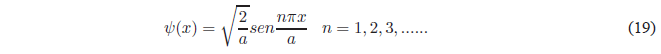 Now we are going to introduce a simple quantum mechanical system, where we can apply the concepts introduced in the previous section. This model can be applied to the one-dimensional translational motion of ideal gas molecules, the motion of electrons in metals, and even the motion of pi electrons in unsaturated hydrocarbons.
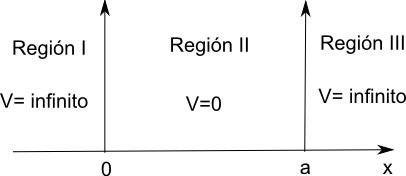
Now we are going to introduce a simple quantum mechanical system, where we can apply the concepts introduced in the previous section. This model can be applied to the one-dimensional translational motion of ideal gas molecules, the motion of electrons in metals, and even the motion of pi electrons in unsaturated hydrocarbons.
Consider a particle of mass m moving along the x-axis subjected to zero potential in the region between the coordinates 0 and a. Outside this zone the potential is infinite. The particle cannot access the zone of infinite potential, so its movement is limited to the region 0,a.
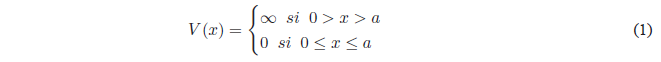
We set up the Schrödinger equation:
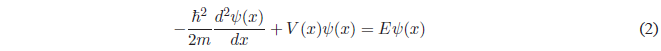
Solving the equation in regions I and III
In regions I and III \(V(x) = \infty\). The Schrödinger equation will take the following form:
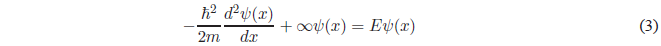
This equation can also be expressed as:
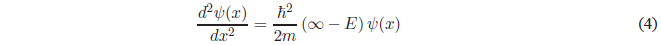
Solving for \(\psi(x)\)
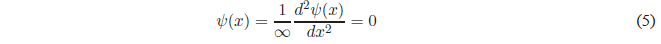
Therefore, in regions I and III the wave function is zero, which implies zero probability density and the particle cannot be found in these regions of the box. A particle cannot be found in regions where the potential energy is infinite.
Resolution of the Schrödinger Equation in region II
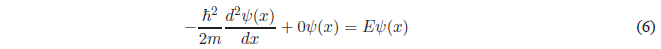
Solving the derivative of higher degree and passing everything to the first member of the equation.
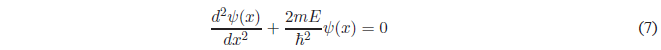
For simplicity we will call \(k=\frac{\sqrt{2mE}}{\hbar}\)
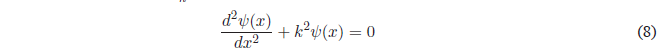
It is a linear, homogeneous, second-order differential equation whose general solution is:
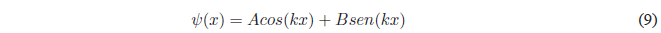
The constants A and B are determined by applying the limit conditions that the function \(\psi(x)\) must satisfy in order for it to be well behaved.
Since \(\psi(x)\) must be continuous, it will satisfy the conditions. \(\psi(x) \rightarrow 0\) if \(x \rightarrow 0\) and if \(x \rightarrow a\). Applying the first condition:
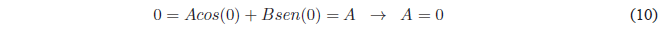
Since $A=0$ the equation remains: \(\psi(x)=Bsin(kx)\). Applying the limit condition on \(x=a\)
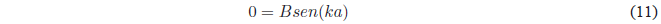
A possible solution of this last equation is \(B=0\), this solution annuls the wave function and would imply that the box does not have a particle
(empty box). Therefore, the \(sen(ka)\) must be canceled
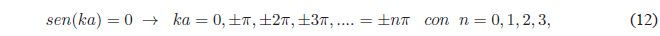
The value \(n=0\) must be rejected since it cancels the wave function.
Squaring the above equation:
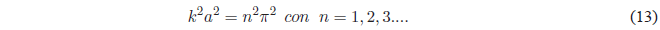
Taking into account that \(k^2 =\frac{2mE}{\hbar^2}\) the previous equation gives us:
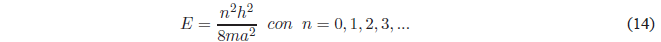
As can be seen in this equation, the energy can only take certain values (quantized energy) that are determined by the quantum number $n$. Only these energy values allow the function \(\psi(x)\) to satisfy the continuity conditions at \(x=0\) and \(x=a\).
Making \(n=1\) we obtain the energy of the ground state \(E_1 =\frac{h^2}{8ma^2}\). It can also be seen that the energy difference between two successive levels decreases as both n and the length of the box increase.
Finally, we will obtain the value of B by normalizing the wave function \(\psi(x)=Bsin\frac{n\pi x}{a}\). Normalizing consists of equaling to 1 the probability of finding the particle in all space.
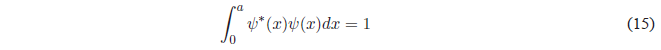
Substituting \(\psi(x)\) for your value:
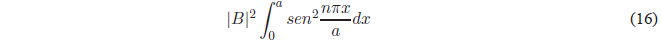
Using the trigonometric relation \(sin^2 x=\frac{1-cos2x}{2}\), we obtain:
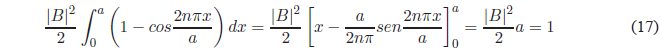
Solving for B
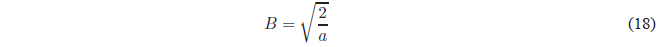
Substituting B into the wave function